Georg Cantor published his theorem in 1891 that the powerset of a set has higher cardinality than the set itself, which theorem transformed the mathematics.
Overview
2012.09.28. 15:26 | Takács Ferenc bp. | Szólj hozzá!
Áttekintő
2012.09.17. 10:11 | Takács Ferenc bp. | Szólj hozzá!
Georg Cantor 1891-ben publikálta tételét a hatványhalmazok nagyobb számosságáról, amely tétel átformálta a matematikát.
The set of rational numbers equal with set of real numbers
2012.09.10. 14:29 | Takács Ferenc bp. | Szólj hozzá!
!!! In January 2025, I made significant discoveries and changes to my theory, so not all of the statements described here are true. I have only left my previous articles to illustrate the development of my thinking. !!!
The rational numbers is determined as quotient of integers. The integers are…
A racionális számok halmaza a valós számok halmaza is
2012.08.23. 11:36 | Takács Ferenc bp. | 5 komment
!!! 2025 januárjában jelentős felismeréseket tettem, és változtattam az elméletemben, így az itt leírt állítások nem mindegyike igaz. Csak a gondolkodásom fejlődésének szemléltetésére hagytam fenn a korábbi cikkeimet. !!!
A racionális számokat az egész számok hányadosaiként határozzuk meg. Az egész…
Páros számok részhalmazának sorszáma
2012.07.23. 10:35 | Takács Ferenc bp. | 3 komment
!!! 2025 januárjában jelentős felismeréseket tettem, és változtattam az elméletemben, így az itt leírt állítások nem mindegyike igaz. Csak a gondolkodásom fejlődésének szemléltetésére hagytam fenn a korábbi cikkeimet. !!!
Többen észrevételezték, hogy azon egy-egy értelmű H(n) leképezésem, amely a…
The refutation of Cantor's theorem
2012.07.20. 17:54 | Takács Ferenc bp. | Szólj hozzá!
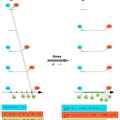!!! In January 2025, I made significant discoveries and changes to my theory, so not all of the statements described here are true. I have only left my previous articles to illustrate the development of my thinking. !!!
Abstract: I show that the set of natural numbers, because incorrect definitions…
A Cantor-tétel cáfolata
2012.07.20. 17:45 | Takács Ferenc bp. | 64 komment
!!! 2025 januárjában jelentős felismeréseket tettem, és változtattam az elméletemben, így az itt leírt állítások nem mindegyike igaz. Csak a gondolkodásom fejlődésének szemléltetésére hagytam fenn a korábbi cikkeimet. !!!
Összefoglalás: Megmutatom, hogy a természetes számok halmaza, hibás…
Mi a matematika
2012.07.19. 16:51 | Takács Ferenc bp. | Szólj hozzá!
!!! 2025 januárjában jelentős felismeréseket tettem, és változtattam az elméletemben, így az itt leírt állítások nem mindegyike igaz. Csak a gondolkodásom fejlődésének szemléltetésére hagytam fenn a korábbi cikkeimet. !!!
Kedves Szerkesztő Úr! Sajnos annak nagyobb része, amit a cikkemmel…
Russell-Cantor analógia
2012.07.19. 16:32 | Takács Ferenc bp. | 5 komment
!!! 2025 januárjában jelentős felismeréseket tettem, és változtattam az elméletemben, így az itt leírt állítások nem mindegyike igaz. Csak a gondolkodásom fejlődésének szemléltetésére hagytam fenn a korábbi cikkeimet. !!!
X halmaz azon elemekből áll, amelyek nem elemei X-nek.
A Russell…
