!!! 2025 januárjában jelentős felismeréseket tettem, és változtattam az elméletemben, így az itt leírt állítások nem mindegyike igaz. Csak a gondolkodásom fejlődésének szemléltetésére hagytam fenn a korábbi cikkeimet. !!!
Összefoglalás: Megmutatom, hogy a természetes számok halmaza, hibás definícióinak (axiómáinak) köszönhetően, nem megszámlálható, azaz kontinuum számosságú, szemben a korábbi feltételezéssel, és szándékkal, mely szerint a természetes számok halmaza megszámlálhatóan végtelen számosságú. A természetes számokat halmazként kezelve nem csupán a megszámlálható nem negatív véges egész számokat tartalmazza, hanem a megszámlálhatatlan számosságú végtelen nagy egész számok osztályát is. Ebből következőleg a megszámlálhatóan végtelen számosságú természetes számok nem alkotnak szabályos matematikai halmazt. Megmutatom azt is, hogy a természetes számok hatványhalmaza szintén nem alkot halmazt, ahogy a természetes számok sem, azonban a hatványhalmaz megszámlálhatóan végtelen részhalmazokból áll, akárcsak a természetes számok. Megmutatom továbbá a Cantor-tétel bizonyításának hibáit.
Kulcsszavak: természetes számok, Peano-axiómák, számosság, hatványhalmaz, Cantor-tétel.
Bevezetés: Amikor Giuseppe Peano 1889-ben publikálta axiómáit, még nem nevezték a természetes számokat halmaznak. Axiómái definiálták, hogy a természetes számok egymásra következnek vég nélkül, és a matematikai indukciót, amely lehetővé teszi a bizonyítást a számelméletben. Két évvel később publikálta Georg Cantor tételét, amely a természetes számokra halmazként hivatkozik. Senkit sem zavart az elmúlt 121 évben, hogy a természetes számok halmazként való használata helytelen, sőt súlyos hibák forrása lehet. Ez a legjobban Cantor tételén, és annak hibás következményein látható. Időközben újrafogalmazták Peano-axiómákat felhasználva a halmazelmélet, így most ezek is hibásan olvashatók a könyvekben. Természetesen a halmazelmélet nagy áldás a matematika számára, mivel könnyen kezelhető, és formalizálható eszközöket biztosít. De a halmazok használata veszélyeket rejt, különösen végtelen halmazok esetében. Ezeket a csapdákat a legnagyobb matematikusok sem tudták elkerülni.
Jelenlegi állapot:
A Peano-axiómák egy jelenlegi változata egyszerű szavakkal:
(P1) a nulla természetes szám,
(P2) minden természetes számra következik egy másik természetes szám (a rákövetkező),
(P3) a nulla egyetlen természetes számnak sem rákövetkezője,
(P4) csak azonos számok rákövetkezői azonosak.
(P5) ha egy halmaz tartalmazza a nullát, és tartalmazza minden elemének a rákövetkezőjét is, akkor a halmaz minden természetes számot tartalmaz.
Megjegyzem, az axiómák ebben a formában, megszabadítva a hibás formalizmustól újra teljesen hibátlanok, bár az ötödik axióma nem egyértelmű.
Következzék Cantor bizonyítása, szintén egyszerű szavakkal:
Tegyük fel, hogy a hatványhalmaz megszámlálható, tehát létezik egy-egy értelmű f(n) megfeleltetés a természetes számok, és a hatványhalmaza között, azaz az f(n) függvény a természetes számok minden lehetséges részhalmazával összerendel egy sorszámot. Most vegyük azt az X részhalmazt, amely azon n természetes számokból áll, amelyek nincsenek a nekik megfelelő f(n) részhalmazban. Tehát, ha mondjuk az 5 nem eleme az ötödik részhalmaznak, akkor az 5 eleme X részhalmaznak. X eleme a természetes számok hatványhalmazának, ezért kell lennie olyan x számnak, hogy f(x) = X, de másrészről X definíciójából következőleg mégsem lehet olyan x hogy f(x) = X. Ez nyilvánvaló ellentmondás, ami azt jelenti, hogy rossz a kiindulási feltételezés. Ezért Cantor úgy véli, hogy a hatványhalmaz nem megszámlálható.
A Cantor-tétel általánosabban is megfogalmazható; egy halmaz számossága kisebb, mint hatványhalmazáé, A bizonyítás hasonló, hiszen a megszámlálhatóságot nem használtuk fel a bizonyításban. Az általános esettel csak az utolsó részben érintőlegesen foglalkozok, mivel elsődlegesen a természetes számok esetével kívánok foglalkozni.
A természetes számok hatványhalmaza megszámlálható
Az azonos számosság bizonyításához elegendő egy egy-egy értelmű leképezés létezését igazolni a természetes számok, és annak hatványhalmaza között. Íme itt egy konkrét leképezés. Vegyük a természetes számok bináris felírását, ahol is csak 0, és 1 található egy szám leírásában, és rendeljük hozzá bármely n természetes számhoz azt a H(n) részhalmazt, amelyben azok a természetes számok vannak, amelyiknél az n adott bináris helyi értékein egyes található. Íme néhány részhalmaz a sorszámaikkal:
H(0) = H(000(2)) = {-,-,-} = {},
H(1) = H(001(2)) = {-,-,0} = {0},
H(2) = H(010(2)) = {-,1,-} = {1},
H(3) = H(011(2)) = {-,1,0} = {0,1},
H(4) = H(100(2)) = {2,-,-} = {2},
H(5) = H(101(2)) = {2,-,0} = {0,2},
H(6) = H(110(2)) = {2,1,-} = {1,2},
H(7) = H(111(2)) = {2,1,0} = {0,1,2},…,
H(15) = H(1111(2)) = {0,1,2,3},...,
H(31) = H(11111(2)) = {0,1,2,3,4}, ..
Ez a leképezés korábban is jól ismert volt, és annyira egy-egy értelmű, hogy nincs is mit bizonyítani ezen. A helyi értékek éppen úgy megszámlálhatóak, mint a természetes számok. A számítástechnikában éppen ez a megfeleltetés teszi lehetővé, hogy a halmazműveleteket bitenkénti logikai műveletekkel valósítsuk meg. A megcáfolásomhoz elegendő lenne bebizonyítani a következő három dolog valamelyikét. Mutatni egy részhalmazt, amelyik nincs hozzárendelve egy sorszámhoz sem, vagy mutatni egy sorszámot, amelyhez nincs részhalmaz rendelve, vagy megmutatni, hogy ez a hozzárendelés nem egy-egy értelmű.
Természetesen a természetes számok hatványhalmaza éppen úgy nem használható halmazként, mint a természetes számok sem. A következő fejezetben megmutatom, hogy ez súlyos hibák forrása lehet. Csak véges számokkal, és a véges számok véges méretű részhalmazaival szabad dolgozni, és a véges esetekre vonatkozó állításokat a matematikai indukcióval lehet kiterjeszteni minden természetes szám esetére. A matematikai indukció nem halmazművelet.
Ez a leképezés felhasználható bármely más megszámlálhatóan végtelen objektumhoz is, például a racionális számokhoz, stb.., mivel ezek egy-egy értelműen hozzárendelhetők a természetes számokhoz.
Ezek után csak az nem világos számomra, hogy ezen trivialitások fényében hogyan lehetett fenntartani ilyen sokáig a Cantor-tétel állításait. Cantor valóban bizonyította, hogy nem létezhet az általa feltételezett függvény, de hibás következtetéseket vont le belőle. De mielőtt erre térnék, előtte egy másik kérdést kell tisztázni.
A véges természetes számok halmaza nem létezik
A természetes számok bármely véges részhalmazának van legnagyobb eleme, aminek rákövetkezőjét nem tartalmazza a részhalmaz, és ennek végtelen sok ezt követő rákövetkezőjét sem (1. tétel). Ha a részhalmaz egy nem-nulla-kezdőszelet, azaz tartalmaz minden természetes számot egytől a legnagyobb elemig, akkor a legnagyobb elem azonos az elemek számával, vagyis az elemek száma eleme a részhalmaznak (2. tétel). Amikor kijelentjük azt, hogy egy halmaz tartalmaz minden természetes számot, ahogy azt látjuk P5 axiómában, akkor a második tétel használatára vagyunk kényszerítve. A természetes számok száma végtelen, így a végtelen is eleme ennek a halmaznak (3. tétel).(kihúzva, és a következő bekezdés beírva: 2016.nov.11.)
A rákövetkezés művelete valamely természetes számról egy másik természetes számra hivatkozik, amelyet újabb természetes számok végtelen sorozata követ. Az egyetlen művelet amellyel a természetes számok bármelyikét elérhetjük az a rákövetkezés művelete, de az, mint látjuk alkalmatlan arra, hogy minden természetes számot elérjünk, bármennyiszer is alkalmazzuk, ugyanúgy végtelen sok természetes számot nem értünk el, tehát kizárólag véges számú természetes számot tartalmazó halmazok érhetők el a rákövetkezés műveletével. A (P5) axióma viszont felveti annak lehetőségét, hogy létezik olyan halmaz, amely tartalmazza az összes természetes számot, jó lehet az a rákövetkezés műveletével nem hozható létre. Vajon hogyan hozható létre ilyen halmaz? Hasonló problémával ismertetett meg bennünket Zénon apóriája. A probléma kezelésére a határérték képzés művelete szolgál mind Zénon apóriájában, mind az összes természetes számot tartalmazó halmaz esetében. Ha egy végtelen sorozat tagjainak mindegyikére szükség van egy művelet elvégzésére, akkor a sorozat határértékét kell képeznünk. N . Az így előállított halmaz azonban nem csak a véges természetes számokat tartalmazza, hanem a végtelen nagy számokat is, mivel az előbbi művelet utolsó eleme .
Tehát amikor hivatkozunk a természetes számok halmazára, vagyis egy olyan halmazra, amelyik minden természetes számot tartalmaz, ez elkerülhetetlenül maga után vonja a végtelen nagy számokra való hivatkozást is. A természetes számok egyetlen véges részhalmaza sem tartalmazhat minden természetes számot, így nincs lehetőség, hogy a részhalmazokat kiterjesszük minden természetes számra a rákövetkezőik, vagy a matematikai indukció segítségével. Nincs középút. Ha azt mondnánk, hogy a végtelen számok nem elemei e halmaznak, akkor ezzel azt is mondanánk, hogy a természetes számok száma véges. Vagy ha azt mondanánk, hogy nem léteznek végtelen nagy természetes számok, úgy az N halmaz képzését még a végtelen előtt be kellene fejezni, de ekkor csak véges részhalmaz lenne az eredmény.
Természetesen azt már tudhatjuk a végtelenről, hogy megszámlálhatatlanul végtelen számosságú halmaz. Bármely végtelen számnak megszámlálhatatlan rákövetkezője van. Tehát amikor végrehajtunk egy műveletet a minden természetes számot tartalmazó halmazon, akkor megszámlálhatatlan végtelen nagy számot tartalmazó halmazzal dolgozunk. Ráadásul a végtelen nagy számok vannak túlnyomó többségben, mivel a véges számok elhanyagolhatóak a végtelen nagy számok számához képest.
Ezt a sajnálatos körülményt nem rögzítik az axiómák, így azok félreérthetők, félrevezetők, és hiányosak.
A végtelen nagy számok leírása megfeleltethető az egynél kisebb pozitív valós számok tizedes törttel való leírása reciprokának, tizedes pontra való tükrözésének. Tehát számjegyek végtelen sorozatával (amit három ponttal rövidítünk) írhatjuk le őket amiket a véges helyi értékek követnek baloldalt. Például a ...00 jelenti a százzal osztható végtelen számokat. Valóban, bármely ilyen végtelen tizedestört a (0,1) intervallumból megfeleltethető ugyanazon számsorozatnak fordított sorrendben, mint egy végtelen nagy egész szám. És mivel ezen végtelen sorozatok megfelelően reprezentálják a valós számokat az intervallumban, így ezek reciproka is megfelelően reprezentálja a végtelen nagy pozitív egészeket, továbbá ezek számossága azonos, tehát megszámlálhatatlanul végtelen.
Ne feledjük tehát, hogy a sokat emlegetett N halmaz kontinuum számosságú, és végtelen számokat tartalmaz. Talán kényelmes leírni a bizonyításokba, hogy n∈N, vagy n∉N, de félrevezető, mivel ∞∈Ν, és ha n végtelen, akkor az n számot tartalmazó formulák gyakran értelmetlenné válnak. Az egyedüli helyes definíció az, hogy „n természetes szám”, vagy hogy „nincs olyan n természetes szám”.
Szerencsétlen következmény, hogy újra kell alkotni a matematikai formalizmust. Bevezethető egy viszonylag egyszerű szimbolikus halmaz, I = N\{∞} és helyettesítve N halmaz I halmazzal, a korábbi képletek döntő többsége korrekt maradna, illetve azzá válna. Természetesen I nem valódi halmaz, így csak korlátozottan végezhetők vele műveletek.
Néhány megjegyzés a Cantor-tételről
A Cantor-tétel cáfolatot nyert azáltal, hogy megmutattam egy egy-egy értelmű leképezést a természetes számok, és hatványhalmaza között. Így itt már csak azt elemzem, hol hibázott Cantor. Az én H(n) leképezésemet használva Cantor bizonyításához ellenőrizhető, hogy az X halmaz minden természetes számot tartalmaz, mivel bármely részhalmaz sorszáma nagyobb, mint a részhalmaz legnagyobb eleme. Így X halmaz a természetes számok halmaza, és a hozzárendelt x sorszám a legutolsó, a legnagyobb véges természetes szám lenne, ha volna ilyen. Ehelyett x végtelen, és láthatólag Cantor végtelen nagy számokkal kalkulál. Cantor előtt a matematika történetében senki sem próbálta végtelen számokat is tartalmazó halmazként kezelni a természetes számokat, és legfőbb ideje felismerni, hogy ezt soha nem is szabad megtenni. A számelméleti problémákat csak indukcióval, és az indukción alapuló módszerekkel lehet bizonyítani.*
A Cantor-tétel nem korlátozódik a természetes számokra, hanem úgy vélik tetszőleges halmazokra lehet alkalmazni, függetlenül azok számosságától. Valójában ezt a tételt tekintik bizonyítékul, hogy a számosságok nem korlátozódnak a természetes számok, és a valós számok számosságára, hanem létezik a számosságok végtelen sorozata is. Ez egy tévedés. Az egy-egy értelmű leképezés létezése bizonyítja két halmaz azonos számosságát, de a leképezés hiánya nem bizonyítja a különböző számosságot. Csak annyi bizonyos, hogy különböző számosságú halmazokra nem létezik ilyen leképezés. A leképezés nem létezésének más okai is lehetnek. Különösen amikor megszámlálhatatlanul végtelen halmazzal van dolgunk. És pontosan ez a helyzet A megszámlálhatóan végtelen esetre megmutattam, hogy létezik ilyen leképezés. Egy halmaz megszámlálhatatlan, ha nem létezik egy-egy értelmű leképezés a halmaz, és a természetes számok között. Nagyon valószínű, hogy ugyanez az oka, hogy nem létezik leképezés a halmaz, és hatványhalmaza között (sejtés).
Szemléltető példa: Keressünk egy hatványhalmazt, és hozzá leképezést a valós számokhoz. Elegendő a [0,1] intervallummal foglalkozni, mivel az intervallum leképezhető a teljes számegyenesre. Osszuk az intervallumot n egyenlő részre, ahol n egész szám, és képezzük az intervallumok hatványhalmazát a fenti H leképezés szerint. Ekkor az n-edik felosztáshoz tartozik 2n sorszám, és ugyanennyi nem folytonos intervallum. Próbáljuk képezni ennek a felosztásnak a határértékét, amikor n tart végtelenhez.
Mit kapunk eredményül? Az intervallumok hosszának határértéke nulla, így az intervallumok valóban valós számokká váltak, és azok folytonosan lefedik a [0,1] intervallumot. (Hasonló lefedést láthatunk a Peano görbénél.) A H leképezés alakulása meglehetősen speciális. Minden véges természetes szám a nullába képez, az intervallum bal oldalán. Az intervallum többi részére csak végtelen nagy természetes számok képeznek. Ugyanis minden véges szám reciproka nullához tart, és így határértéke nulla. Azonban ez a leképezés nem egy-egy értelmű, mivel minden véges természetes szám az egyetlen egy nullába képez. A helyzet még rosszabbul alakul a hatványhalmaz esetére, mivel az nem konvergál. A különböző felosztásokhoz tartozó hatványhalmazok függetlenek egymástól. Így ez a példa azt mutatja, milyen problémás hivatkozni egy megszámlálhatatlan halmaz hatványhalmazára, vagy leképezni azt. Nagy valószínűséggel áthidalhatatlan nehézség. Ezért a hatványhalmaz fogalmának használata nem megalapozott megszámlálhatatlan halmazoknál. Még kevésbé megalapozott leképezést rendelni egy ilyen gyanús halmazhoz. Nem találtunk megoldást, de a hitünk erősödött abban, hogy nincs is megoldás.
Ez a példa azt is megmutatta, hogy miképpen törpül nullává a megszámlálható számosság a megszámlálhatatlanhoz képes. Ezzel szemben nagyobb számosságok nincsenek, és nincs rájuk példa. Ez csak téves hipotézis. Nincs nagyobb számosság, mint a valós számok számossága.
Ez a példa azt is megmutatta, hogy a természetes számok halmaznak nyilvánítása maga után vonja a határértékképzést, mivel a halmaz, és vele a végtelen nagy számok nem kaphatók meg indukcióval. Ezt nem árt még egy példán bemutatni.
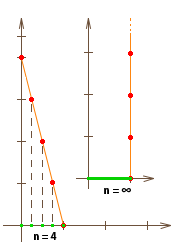
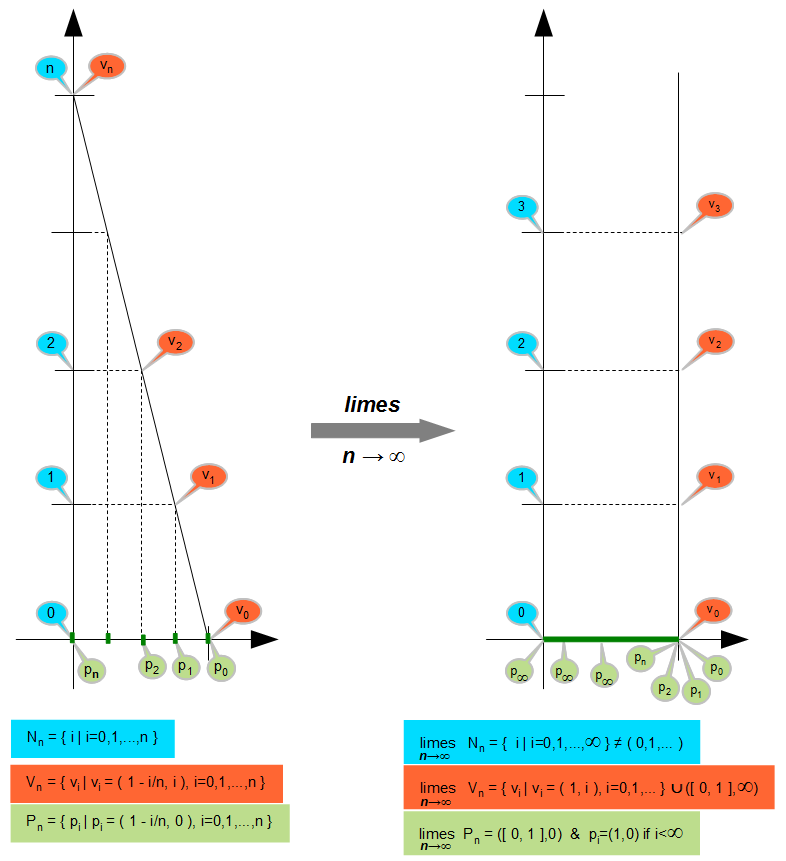
Még egy példa: (A végtelen létra vetülete) Állítsunk szimbolikus létrákat (illetve azok elvi metszeteit, tehát egyenes szakaszokon egyenletes távolságra eső pontsorozatokat) az (1,0) koordinátájú pontba úgy hogy a létrákat az y tengelynek támasszuk. Bármely létra mindig olyan hosszú, hogy az y tengelyt pozitív egész értékeknél éri el, és a létrafokok y koordinátái is mindig egész számok. A létrákat az y tengellyel való metszés szerint indexeljük, így az n-edik létra az y=n–nx egyenletű egyenes y tengely és x tengely közötti szakaszán levő egész y koordinátájú pontokból áll. Vizsgáljuk a létra fokok x tengelyen való x vetületeit is. Az n-edik létránál ezek a (k/n,0) koordinátájú pontok, ahol (k=0,...,n).
Vizsgáljuk meg mihez konvergál a létrák sorozata, a létrafokok vetülete, és a létrafokok y koordinátáinak halmaza, mikor n-nel tartunk végtelenhez. A létra n növekedésével egyre meredekebb lesz, és a függőlegeshez konvergál, így határértékben függőleges pontsorozat lesz (1,0) felett. A létrafokok vetületei közti távolság 1/n szerint nullához konvergál, tehát határértéke nulla, így a létra vetülete határértékben folytonosan lefedi a [0,1] valós intervallumot. A létrafokok y koordinátáinak halmaza sorra a természetes számok kezdőszelet halmazai, és ennek határértéke tartalmazza az összes véges természetes számot. De nem csak azokat. Ugyanis tetszőleges véges k természetes számra az 1-k/n vetület egyhez konvergál, amikor n tart k-tól végtelenhez, így minden véges indexű lépcsőfok az egyetlen (1,0) vetületi pont fölé esik. A [0,1] intervallum többi részére, ami [0,1) intervallum, következésképpen csak a végtelen nagy egész számokkal indexelt lépcsőfokok vetületei eshetnek. Így hát ezen végtelen nagy természetes számok is szükségképpen elemei a halmaznak. A példa igen szemléletesen megmutatja, hogy egy végtelen sorozat kizárólag a határértékképzés művelete által válhat halmazzá, de közben a megszámlálhatóan végtelen sorozat megszámlálhatatlan folytonos sokasággá válik.
Még egy következtetés: Felmerülhet a kérdés, mi szükség az ötödik axiómára. Némely forrás szerint az indukció elvét hivatott deklarálni. Ha ez így lenne, akkor ez nagyon rossz út erre. Egy axióma csak akkor lehet jó, ha magától értetődő, és az elemi matematikai oktatás alapja tud lenni Nagyon hasznos, ha tudjuk milyen műveleteket lehet végezni véges halmazokkal, de súlyos hiba, ha a természetes számokat halmaznak tekintjük. Ez nem elemi matematika, nem az axiómák szintje.
Budapest, 2012. május 21.Takács Ferenc bp.
* Mint ahogyan a későbbi cikkeimben részletesen rávilágítottam, Cantor bizonyítása minden részletében pontosan megfeleltethető a Russell paradoxonnak, és pontosan azért nevezzük ezt a logikai bakugrást paradoxonnak, mert logikailag ellentmondásos feltevéssel hozz ki egy logikai ellenmondást. Cantor ugyanis egy olyan halmazt próbál kreálni a bizonyításban, amelybe csak azok az elemek kerülhetnek be, amelyek nem lehetnek az elemei, tehát ellentmondásos a feltétel. Ily módon azután könnyű kimutatnia, hogy ilyen halmaz nem is létezhet, csak hogy ennek semmi köze a bizonyítandó tételhez, sőt még a halmazelmélethez sem. Egy szimpla logikai hibáról van szó.