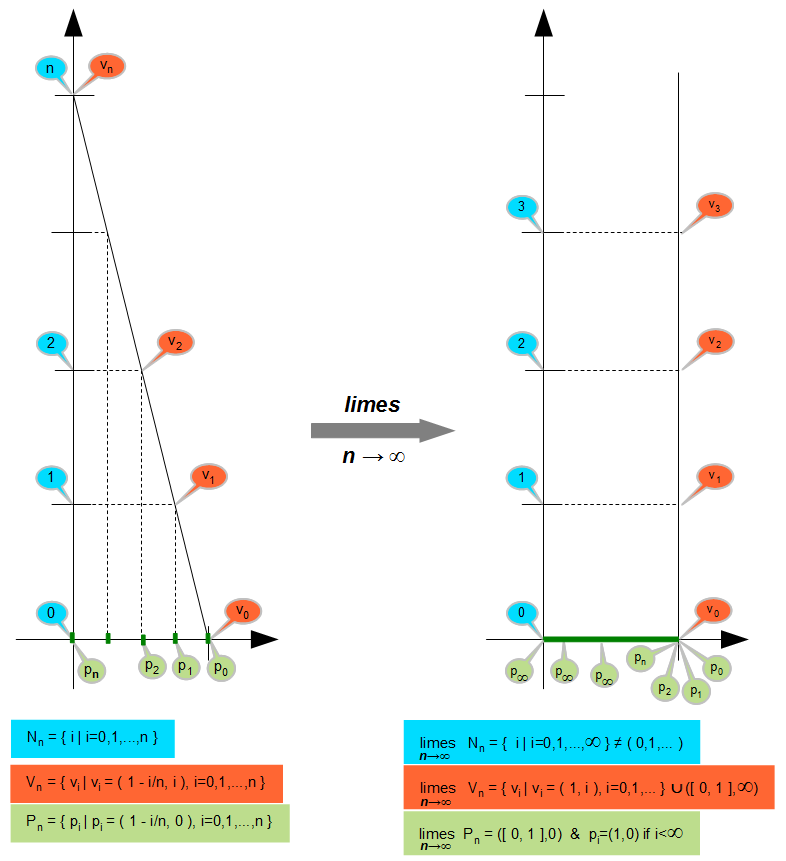
Itt egyszerű ponthalmazok leképezése látható. Az egyik ponthalmaz a természetes számok kezdőszelet halmazai (N), a másik halmaz (V) a függőleges tengelynek támaszkodó egyenes egész koordinátákat metsző pontjai, a harmadik ponthalmaz (P) ezek vetülete a vízszintes tengelyen. Az egyenes a vízszintes tengelyt az egyes értéknél metszi, a függőleges tengelyt pozitív egész koordinátáknál, és ez a koordináta érték a ponthalmaz indexe. Az indexek szerint a halmazok sorozatát képezzük, majd ezen sorozatok határértékét.
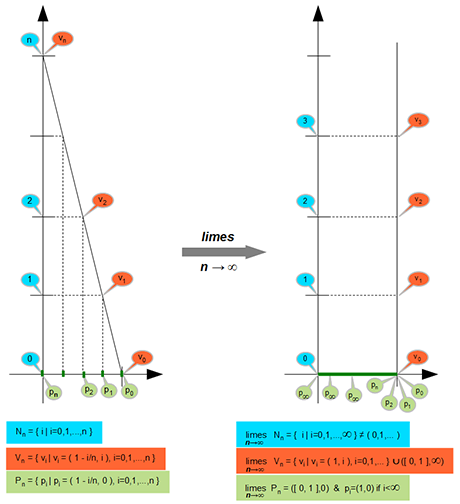
Az első képen tehát két leképezést ( N=>V és V=>P) ábrázolunk, a második képen ezek határértékét.
A sorozatok határérték képzéséből kiderül, hogy az indexhalmaz, vagyis a véges természetes számok sorozata nem képez rá a határérték halmazra, ugyanis a pontvetületek halmazainak határértékhalmaza a valós számok folytonos intervalluma, míg a létrapontok határértéke az egyes koordináta feletti függőleges pontsorozat, és e pontsorozat minden véges indexű vetülete az egyes koordinátájú pont. Tehát önként adódik az a megoldás, hogy az intervallum további részére, ami egyetlen pont kivételével a teljes intervallum, a végtelen nagy értékű indexek képeznek rá. Ezzel feloldódik az az ellentmondás is, hogy a megszámlálhatóan végtelen véges indexek nem képezhetnek rá egy megszámlálhatatlan végtelen folytonos intervallumra. Valóban nem képeznek rá, hiszen a véges indexek egyetlen pontra képeznek, és a folytonos intervallumra csak a végtelen nagy indexek képeznek, amelyeknek számossága tehát szintén megszámlálhatatlanul végtelen.
Ez egyben azt is jelenti, hogy a véges természetes számoknak csupán a sorozata (amit a rákövetkezések műveletével definiálunk) megszámlálhatóan végtelen, az összes természetes számok halmaza, amit e sorozat határértékeként kaphatunk, megszámlálhatatlanul végtelen, és tartalmazza a végtelen nagy számokat is. Ennek okából a természetes számok halmazára való hivatkozások maguk után vonják a végtelen nagy számokra való hivatkozást is, amit általában nem kívánatos, hiszen nem végezhetők el velük mindazok a műveletek, amik a véges számokkal elvégezhetők. Ugyancsak probléma a racionális számok halmazként való emlegetése, hiszen a végtelen nagy számok jelenléte miatt ez a halmaz azonos a valós számok halmazával. Tehát a racionális számok is csak sorozatként definiálhatók értelmesen, nem pedig halmazként.
Hogy jobban érthessük a végtelen halmaz, és a sorozat fogalma közötti különbséget, gondoljunk csak a teljes indukció elvére. Ez az elv adja a kulcsot a véges természetes számok körében megfogalmazott számelméleti problémák bizonyításához. A teljes indukció elve tökéletes összhangban van a sorozat fogalmának definiálásával, ami persze nem meglepő, hiszen a természetes számok sorozatot alkotnak, és a teljes indukció elve azt a követelményt állítja elénk, hogy egy bizonyítandó állításból is alkossunk állításokból álló végtelen sorozatot, amely így tagonként rendre megfeleltethető a természetes számok sorozatának, tehát minden természetes számra érvényes így az állítás. Ez a követelmény szükséges és elégséges feltétele egy állítás igazságának bizonyításához. Ez egyben azt is jelenti, hogy minden további követelmény felesleges, és hibás a természetes számok körében tett kijelentéseket illetően, gondolok itt elsősorban a természetes számok sorozatának halmazként való kezelésére. Hiszen látható fent a végtelen létra példájából, hogy a V határérték halmazban nem különíthetők el határozottan a véges, és végtelen indexű tagok (bár állíthatjuk, hogy minden véges indexű tag x koordinátája 1, de nem állíthatjuk, hogy minden 1-es x koordinátájú tag véges indexű), tehát az összes véges természetes szám sem különíthető el határozottan a végtelen nagy számoktól sem, így egy ilyen halmaz elemeivel nem számolhatunk úgy, mintha azok csak véges természetes számokból állnának.
Ezzel szorosan összefügg az is, hogy sorozatok, és végtelen halmazok esetében a hatványhalmaz (illetve annak sorozata) ugyanolyan számosságú, mint az alapsorozat, illetve halmaz, tehát Georg Cantor tétele, amely ennek ellenkezőjét állítja, hibás.
Budapest, 2013. április 26.
