Az itt definiált fogalmak bár hasonlítanak a máshol definiált azonos nevű fogalmakhoz, de többnyire nem azonosak vele, sőt lényegbevágó eltérések is vannak, így vigyáznunk kell arra, hogy milyen környezetben használjuk, mert más környezetben durva hibák, és félreértések adódhatnak a definíciók eltéréseiből. A rövid leírás célja éppen az, hogy ezek a gondolatok összehasonlíthatók legyenek a máshol szokásosakkal. Mindemellett sok olyan kérdésre nem térek ki, amelyek a szokásos tárgyalásmódból jól ismertek, vagy megismerhetők.
Utolsó módosítás: 2025.03.04.
Alapfogalmak
Mivel mondanivalóm kizárólag a halmazok, a számosságok, és a természetes számok értelmezését érinti, így néhány más területet érintő előzetes matematikai alapfogalom definícióiról nem lesz szó, azokat előzetesen ismertnek tételezem. Ezek a matematikai logika, matematikai kijelentések, és relációk alapszintű ismeretei, a leképezések, és egy-egy értelmű leképezések fogalmai. Ezek nagyrészt a hétköznapi nyelv logikájának pontosított megfogalmazásai, és magam sem kívánok ezek alkalmazásába mélyebben belemenni, így talán nincs szükség komolyabb előtanulmányokra ahhoz, hogy írásom érthető legyen bárki számára. Az új matematikai fogalmakat fokozatosan fogom bevezetni, lehetőleg ügyelve, hogy először csak az egyszerűbb ismereteket tárgyaljam, és csak ezek után, ezekre támaszkodva jussak el a bonyolultabb ismeretekig. Emiatt, mint látni fogjuk, bizonyos matematikai struktúráknak lesz egyszerűbb, és bonyolultabb, teljesebb változata is. Az ismeretek bővítésének eme lépcsőzetes, egyre elmélyültebb tárgyalási módja mélyebb filozófiai megfontolásokra is visszavezethető, mivel csak ezen a lépcsőzetes módon lehet logikailag korrekt módon felépíteni a tudásunkat akár matematikai, akár más területen. A matematika (axiomatikus) megismerésének útja többféle lehet, különösen ha már több alapfogalmat ismerünk, így nem állítható, hogy az itt leírt út lenne az egyetlen lehetséges út, ugyanakkor fontos tudnunk, hogy itt egészen új megközelítéssel találkozhatunk. A jelenlegi axiómarendszerek egy lépésben akarnak mindent teljes mélységükben definiálni, és ezért átláthatatlanul, ellenőrizhetetlenül bonyolulttá válik már az elmélet megalapozása is. Ahogy mondják, aki sokat markol, az keveset fog.
A véges számosságú halmaz definíciója
A halmaz tetszőleges objektumok csoportja, amelyben az egyes megkülönböztethető objektumokat a halmaz elemeinek nevezünk. A halmazt az elemei egyértelműen meghatározzák, és fordítva; a halmaz egyértelműen meghatározza az elemeit. Az olyan csoportot, amelyben az objektumok hozzátartozása nem határozható meg egyértelműen, nem nevezhetjük halmaznak. Az olyan objektumokat, amelyek összetartozását nem tudjuk egyértelműen meghatározni, nem alkotnak halmazt. Találkozunk olyan paradox halmazdefiníciókkal, amelyek ellentmondásra vezetnek a tartalmazást illetően, vagyis a tartalmazásból következik a nem tartalmazás igénye, és a nem tartalmazásból a tartalmazás igénye. Ezek hibás logikai definíciók, és az így definiált halmazok logikailag nem létezhetnek. Tehát a halmazhoz tartozás meghatározásának egyértelműsége szükséges feltétele egy halmaz létének. Egy halmazba kiválasztott objektumokat az teszi halmazzá, hogy kiválasztottuk őket, vagyis a halmaz egy tisztán absztrakt fogalom, amelynek elemei lehetnek akár fizikailag létező dolgok, vagy akár az elemek is lehetnek absztrakt fogalmak. A halmaz elemeinek különböznie kell egymástól. Az olyan halmazhoz hasonlatos matematikai struktúrákat, amelyben azonos elemek többször előfordulhatnak, nem halmazoknak, hanem multihalmazoknak nevezzük, és magasabb szinten tárgyalja a matematika, jelen írásban nem tárgyaljuk, csupán a teljesség kedvéért szükségesnek tűnt itt megemlíteni a fogalom ezen szűkítésének okát. Azáltal, hogy nem engedjük meg a halmazban az elemazonosságot, jelentős egyszerűsítést jelent a továbbiakban, ami megkönnyíti a halmazok elméletének megismerését. Más tekintetben a halmazt alkotó objektumok bármik lehetnek. Tárgyak, fogalmak, bármi. A leírtakban bárki ráismerhet az un. naiv halmazelmélet alapjaira, de kezdésnek csak a véges számú elemet tartalmazó halmazokat vesszük. A halmazelmélet kiterjesztésére akkor kerülhet sor, ha az ehhez szükséges fogalmak (végtelen) definiálásra kerültek. Példának okáért, ha kavicsokat rakosgatunk egymás mellé, hogy halmazt alkossanak, akkor feltételezzük (egyébként teljes joggal), hogy nincs két egyforma kavics, és csak véges számú kavics hozzáférhető számunkra.
Jelölések:
Legyen H egy halmaz, amelynek elemei a, b, c, és d.
Ezt úgy jelöljük, hogy H = { a, b, c, d }.
Így jelöljük azt, hogy a eleme H halmaznak: a ∈ H
Van egy univerzális speciális halmaz, az üres halmaz {} = ∅, amely nem tartalmaz elemet. Univerzális, mert bármilyen objektumokat tartalmazó halmazból eltávolítjuk az elemeit, akkor ugyanehhez az üres halmazhoz jutunk.
Részhalmaz: A ⊆ B, A halmaz minden eleme B halmaznak is eleme.
Valódi részhalmaz: A ⊂ B, A halmaz minden eleme B halmaznak is eleme, de B halmaz nem minden eleme eleme A halmaznak.
Egy halmaznak elemei lehetnek maguk is halmazok.
Például a C = { {}, {{}}, { {}, {{}} } } is halmaz, de az elemei csupán az üres halmazból képezett különböző halmazok, vagyis egy tisztán matematikai absztrakció a halmaz itt definiált tulajdonságai alapján.
Műveletek:
Halmazegyesítés, vagy unió: { a, b, c, d } ∪ { c, d, e, f } = { a, b, c, d, e, f }
Közös rész, vagy metszet: { a, b, c, d } ∩ { c, d, e, f } = { c, d }
Különbség, vagy kivonás, vagy eltávolítás: { a, b, c, d } \ { c, d } = { a, b }
E műveletek világosan mutatják, hogy az azonos jelölésű elemek egy, és ugyanazt az elemet jelentik.
Véges halmazok számosságáról:
Ha két halmaz elemei között egy-egy értelmű megfeleltetés létesíthető mindkét halmaz összes elemére vonatkozóan, akkor a két halmaz azonos számosságú. Ha ilyen megfeleltetés csak az egyik halmaz minden elemét érinti, míg a másik halmaz elemeinek csak egy részét, akkor a másik halmaz nagyobb számosságú, míg az egyik kisebb számosságú. A valódi részhalmaz kisebb számosságú. Az üres halmaz számosságánál nincs kisebb számosság, ez egyben a legkisebb számosságú halmaz. Az azonos számosságú halmazok meghatároznak egy-egy ekvivalencia osztályt, vagyis a halmazok számosságuk szerint ekvivalencia osztályokba sorolhatók. A kisebb, vagy nagyobb számosság alapján az ekvivalencia osztályokon rendezést tudunk értelmezni. A számosság fogalmára még gyakran visszatérünk. A halmazok fogalmához ismeretelméletileg hosszú folyamat vezet a különböző dolgok véges csoportosítási lehetőségeinek elemzése, gyakorlása révén, de feltételezzük, hogy ezek már nem szorulnak magyarázatra cikkünk olvasóinak.
Az egyszerű sorozat definíciója:
Az egyszerű sorozat egy összetett matematikai alap-objektum, amelynek tagjai vannak. A tagok között van egy kitüntetett tag, amelyet kezdő tagnak nevezünk. Az egyszerű sorozatban definiálunk egy rákövetkezési szabályt, amely a már definiált tagok alapján bármely tagra következő olyan rákövetkező tagot definiál, amely nem lehet azonos semelyik korábban definiált taggal. Egyszerűbb esetekben az első néhány tag felsorolásával, és ... jelzéssel is megadhatunk sorozatot zárójelbe zárva,ha az nem okoz félreértést (0,2,4,6,8,…) a páros számokra, vagy (1,2,4,8,16,…) a kettő hatványaira. A rákövetkezési szabály tehát minden már definiált tagra definiál egy újabb előzőktől különböző rákövetkező tagot, így az egyszerű sorozatnak nem lehet vége, csak kezdete, és folytatása, vagyis végtelen. A korábban példának felhozott kavics halmaz esetében tehát olyan feltételezéssel élünk, hogy nincs semmilyen elvi korlátja, hogy újabb, és újabb előzőektől különböző kavicsokat tegyünk a kavics halmazhoz, ami persze csak elvileg képzelhető el, a valóságban megvalósíthatatlan, valamint pontosan nyilvántartjuk, milyen sorrendben kerültek a kavicsok a halmazba. Az egyszerű sorozat tetszőleges, definiált tagjai alkothatnak véges halmazt, amelyet a tagokból alkotott részhalmazoknak nevezzük. Az olyan részhalmazt, amelyben benne van a kezdő tag, és egy adott tagig bezárólag a kezdő tagra következő összes tag, az egyszerű sorozat adott taghoz rendelt kezdőszelet halmazának nevezzük. Az adott tagra következő tag már nem eleme ennek a kezdőszelet halmaznak. A kezdőszelet részhalmazok véges számosságú halmazok. Mivel a véges halmazok elemei a korábbiak szerint bármik lehetnek, ha azok meghatározása egyértelmű, így az egyszerű sorozat tagjaira sincs más korlátozás, tehát bármik lehetnek, ha a rákövetkezési szabály egyértelműen definiálja őket. Az egyszerű kitétel azért szerepel, hogy a speciális kivételekkel, vagy a később tisztázandó általános sorozat fogalmával ne kelljen most foglalkozni. Tekintsünk ezután egy fontos, és konkrét egyszerű sorozatot.
A számosság-generátor S sorozatának axiómái:
-
AX1: Az S sorozat tagjai halmazok.
-
AX2: Legyen az S sorozat kezdő tagja az üres halmaz. {} = ∅.
-
AX3: Minden s taghoz tartozik egy rá következő s+ tag, amely egy új elem hozzáadásával (uniójával) különbözik az s tagtól, és ez az új elem az s tagot tartalmazó halmaz: s+ = s ∪ {s}
A matematika tudománya alap-axiómáinak olyan különleges feltételeknek kell eleget tenniük, amelyek biztosítják, hogy a matematika minden más tudomány, és így a valóság megismerésének is szilárd alapot biztosítsanak. Ezért ezeknek a definícióknak magától értetődőknek kell lenniük, a legkisebb kétséget sem hagyva igazságtartalmukat illetően. Minden más bonyolult, és elvont matematikai állítást a későbbiekben az axiómák igazságára alapozva vezetünk le lépésről lépésre, de az axiómákat már nem tudjuk még egyszerűbb állításokra visszavezetni, ezért azoknak egyszerűknek, és magától értetődőknek kell lenniük. Ennek ellenére ugyanazt a definíciót gyakran alternatív módokon is meg lehet fogalmazni, de ez a lényegen nem változtat. Természetesen már az alap-axiómák megértése is feltételezi a világunk, a beszélt nyelv valamilyen szintű ismeretét, és absztrakciós képességet, amire fel lehet építeni a további absztrakciókat.
Következmények:
-
∅ ∈ S ∧ a ∈ S → a ∪ {a} ∈ S.
-
Néhány tag az elejéről:
{},
{{} },
{{},{{}} },
{{},{{}},{{},{{}}} },
…
Mint láthatjuk, a számosság generátor sorozat egy egyszerű sorozat, amely csak matematikai fogalmakra épülő absztrakció. -
A sorozatra szokásos (,,...) jelölést használva: S = ( {}, {{}}, { {}, {{}} }, { {}, {{}}, {{},{{}}} }, … ) .
-
Alternatív definíció: minden következő sorozat tag megegyezik a megelőző sorozat tagokból képzett (vagyis kezdőszelet) halmazzal. Ez mind 2., mint a 3. axiómát is helyettesíti, hiszen az első tagra is igaz, mivel az első tagot megelőző sorozat a semmi, így a belőle képzett halmaz az üres halmaz.
-
Minden tag eggyel több elemet tartalmaz, mint az előző tag.
-
Minden tag különböző.
-
Minden tag véges sok elemet tartalmazó halmaz.
-
A sorozatnak nincs vége, a 3. axióma eljárása bármeddig folytatható, vagyis az S sorozat végtelen.
-
Minden a tag halmaz számossága kisebb, mint a rá következő a+ tag halmaz számossága.
-
Bármely véges számosságú halmaz számossága megegyezik az S sorozat valamely tagjának számosságával. A bármely kitétel itt nem csak matematikai objektumokat jelent, hanem a világunk tetszőleges elemeiből, fogalmaiból képezett véges számosságú halmazokat is. Ezáltal válik a matematika a természettörvények leírásának nyelvévé.
-
Az S sorozat minden véges számosságú halmazzal megegyező számosságú halmazt tartalmaz. Vagyis bármely véges számosságú halmaz számossága jellemezhető az S halmaz valamely tagjával. A számosság ekvivalencia osztályokat jelent az azonos számosságú halmazok között, illetve egy rendezést is definiál az S sorozat tagjainak sorrendje szerint ezekre az ekvivalencia osztályokra.
-
Nincs olyan tag, amelynek számossága megegyezne az S sorozat számosságával, mivel az S sorozat számossága végtelen, de S minden tagjának véges a számossága. Tehát a számosság fogalma egy újabb értékkel bővült, a végtelennel, pontosabban a felsorolható, vagy megszámlálható végtelennel. Ez a számosság minden véges számosságnál nagyobb.
-
Az S sorozat minden taghalmazához rendelhető egy számnak nevezett matematikai objektum egy-egy értelműen, amely egyben a tag halmaz számosságával is azonos. Ez a hozzárendelés definiálja a véges természetes számok végtelen sorozatát. Vegyük észre, hogy a természetes számokat sorozatként definiáltam és nem halmazként, ahogyan az elterjedt Georg Cantor munkássága óta, és fennmaradt az azt követő axióma rendszerekben is! A jelenlegi új axiómarendszerben a végtelen fogalma a sorozatok befejezhetetlenségén keresztül kerül be itt a matematika fogalmai közé, mintegy a bármely, tetszőleges véges eset fogalmának szinonimája. Minden véges természetes számhoz egy-egy értelműen hozzá van rendelve egy véges számosságú halmaz, amelynek számossága jellemzi a hozzárendelt természetes számot is, ezenkívül a rákövetkezés axiómája összekapcsolja a természetes számokat, mint egy sorozat tagjait. Az S sorozat kezdő tagjának, az üres halmaznak a számossága, illetve a hozzárendelt természetes szám nulla, és minden következő taghoz rendelt természetes szám nagyobb az előző természetes számnál, vagyis a természetes számokon is értelmezve van a rendezés. A számokon ezeken kívül lehet értelmezni aritmetikai műveleteket a rákövetkezés műveletéből származtatva, lehet értelmezni a felírásukat néhány számjegy szimbólum adott módszer szerinti hozzájuk rendelésével, amelyre következő pontban térek ki, bár mondanivalómtól függetlenek, és csupán további összefüggéseket definiálnak az itt definiált sorozat tagjai között. Az itt szereplő axiómák a természetes számok Neumann-féle modelljéhez hasonlatosak, s szimbólumok arra emlékeztethetnek, de más logikai felépítés, és következtetések szerint. A számosság-generátor S sorozat bár ekvivalens a természetes számok sorozatával, mégsem azonos vele, legfőképpen azon célból, hogy a két sorozatot fogalmilag is elkülönítsük, de meg is feletessük egymásnak, így emlékeztetve minket arra, hogy a természetes számok mindegyike adott számosságú halmazok osztályainak fogalmi elvonatkoztatásai. Ez az összerendelés, és elvonatkoztatás történelmileg, és ismeretelméletileg is megegyezik a számfogalom kialakulásával. A két fogalom elkülönítése lehetővé teszi, hogy a természetes számokat olyan egyszerű sorozatként kezeljük, amelynek tagjai nem halmazok, csupán a számleírás szabályait követő szimbólumok, vagy egyéb szimbolikus jelölések. De jegyezzük meg, hogy a számok szimbólumai valójában adott számosságú halmazok absztrakciói.
-
A természetes számok N sorozatának tízes számrendszerbeli definíciói:
Legyen a számjegy szimbólumok halmaza a következő: {0,1,2,3,4,5,6,7,8,9}, vagy szavakkal {nulla, egy, kettő, három, négy, öt, hat, hét, nyolc, kilenc}. Ezen halmaz elemeit a következők szerint rendeljük a számosság-generátor S sorozathoz.
∅ ↔ 0, vagyis az első természetes szám a 0.
∅+ ↔ 1, vagyis a következő természetes szám az egy,
( s ↔ n ) → ( s+↔ n+1 ), vagyis a rákövetkezés művelete a +1 műveletnek, azaz az egyes szám hozzáadásának felel meg, és s a számosság-generátor S sorozat tagja, n a természetes számok N sorozatának a tagja.
0+1=1, 1+1=2, 2+1 =3, 3+1=4, 4+1=5, 5+1=6, 6+1=7, 7+1=8, 8+1=9, vagyis ez az egyjegyű számok sorrendje. A további számokat több számjegy egymás után írásával jelöljük meghatározott szabályok szerint. A jobb oldalon van a legkisebb helyi-érték, amelyen a számjegyek minden egyes hozzáadásával egyet változnak. Ha ez a számjegy 9-es, akkor a rá következő számban a jobboldalon a 0 következik, miközben az eggyel balra eső helyi-értéken, ha ott még nincs számjegy, akkor 1-et írunk, de ha már számjegy szerepel, akkor eggyel megnöveljük ezt a jegyet, mintha a jobboldalon levő számot nem vennénk figyelembe. Vagyis a kilences után mindig egy átvitel keletkezik a következő helyi-értékre (balra). Az új helyi-értékek bevezető számai, és azok nevei rendre 10 tíz, 100 száz, 1000 ezer, 10000 tízezer, 100000 százezer, 1000000 egymillió, 10000000 tízmillió, ... Észrevehetjük, hogy itt egy újabb sorozat definícióval állunk szemben, amelyet bár összerendeltünk a számosság-generátor sorozattal, de attól függetlenül is definiálható. Hasonló módon eltérő számú szimbólumra alapozva más számrendszereket is lehet definiálni, és gyakran használunk is ilyen számrendszereket a számítástechnikában, és a számelméletben. Ezek a definíciók ekvivalensek egymással, vagyis mindegyike ugyanúgy a természetes számok sorozatát definiálja, de a számosság-generátor sorozat definíciója mutatja meg legjobban a számfogalomban rejlő absztrakciót.
A + jelet eddig csak az 1 hozzáadásával kapcsolatban használtuk, de ez egyben az összeadás jele is, amit általánosabban így definiálunk: x+(y+1) = (x+y)+1, vagyis egy számhoz egy másik szám rákövetkezőjének összege megegyezik az összeg rákövetkezőjével. Ebből levezethetők az összeadásra vonatkozó fontos szabályok, például a+b=b+a (kommutativitás), vagy (a+b)+c=a+(b+c) (asszociativitás). A természetes számok sorozatán a szorzás műveletét is értelmezzük: x·(y+1) = (x·y)+y, vagyis egy számot egy másik szám rákövetkezőjével megszorozva a szorzat, és a másik szám összegét kapjuk. Hasonló szabályok itt is levezethetők. a·b=b·c (kommutativitás), (a·b)·c=a·(b·c) (asszociativitás). Továbbá mindkét művelet szerepeltetése esetére (a+b)·c=(a·c)+(b·c)=a·c + b·c (disztribúció, vagy kiemelés). A végén alkalmaztuk a műveletek elvégzési sorrendjére kikötött szabály (a szorzást az összegzés előtt végezzük el), így a zárójeleket elhagyhattuk. Természetesen az itt szereplő definíciók számos más alternatív módon is megadhatók, amelyekkel számos más helyen találkozhatunk. Ezek a természetes számokra vonatkozó aritmetikai alapműveletek definíciói, amelyek segítségével számolni tudunk. További műveleteket is szokás definiálni, mint összehasonlítás, kivonás, maradékos osztás, maradék képzés, hatványozás, és így tovább, de ezekkel itt nem foglalkozunk. De egy sorozat bizonyos tagjainak összeadására gyakran használjuk a szumma összegző jelet, például
vagy
- Ha a számrendszerek leírása definiált, akkor az S sorozat leírása egyszerűsödik:
0 = {},
1 = {0},
2 = {0,1},
3 = {0,1,2},
...,
n+ = {0,1,2, ..., n} , vagy más jelöléssel n+=
...
Jól látható ezen, hogy a számok valóban megfelelnek a kezdőszelet halmazoknak. -
Az itt definiált sorozatok képezik az alapját a matematikai számelméletnek. A tagok szabályos egymásra következése teszi átvihetővé a számelmélet különféle állításait a természetes számok teljes sorozatára, vagyis minden természetes számra. A legismertebb bizonyítási forma a számelméletben a teljes indukció, amikor is egy adott természetes számra igazolunk egy állítást, majd azon feltételezés mellett, hogy az állítás tetszőleges számra igaz, igazoljuk azt is, hogy az állítás a következő természetes számra is igaz marad. A teljes indukció képezi az alapját az egyszerű sorozat definíciójának is, valamint a felsorolt következményeknek is. A teljes indukció elve, és a fenti axiómák tehát egyenértékűek, nincs szükség újabb axióma kimondására, hogy a teljes indukció elve érvényesüljön. A számelméleti állítások tehát véges természetes számokra vonatkoznak, és véges számú természetes számot, és véges számban elvégzett műveletet használnak fel a bizonyításokban, jó lehet, az nincs meghatározva, és nem is lehet meghatározni, milyen, és mennyi véges számról is van szó, mivel ezek számossága nem véges.
Az általános sorozat definíciója
A természetes számok sorozatának tagjaihoz valamely függvénnyel hozzárendelt függvényértékeket sorozatnak nevezzük. Mint fentebb láttuk, a természetes számok sorozatát is a számosság-generátor sorozathoz való egy-egy értelmű hozzárendelés eredményeképpen kaptuk, ezért itt akár a számosság-generátor sorozatra is hivatkozhatnánk, de a természetes számokra hivatkozó hagyományosabb definíció is ugyanúgy megfelel, mivel a megfeleltetés egy-egy értelmű. A természetes számok rákövetkezése alapján nevezzük a sorozat tagjait egymás után következőknek. A sorozatok értékkészletének számossága vagy megszámlálható végtelen, vagy véges. A véges számosságúakat csak a tagokat egyedivé tevő indexelés miatt nevezhetjük sorozatoknak, az indexelést elhagyva már nem sorozatok, hanem csak véges számosságú halmazok. Az ilyen véges értékkészletű sorozatokban több tag azonos értékű, és ezek végtelenszer ismétlődnek, hiszen az indexelés (a tagok sorszámozása) nem véges. Minden teljes indukciós bizonyítás is egy-egy sorozat definícióját, és a definíció helyességének bizonyítását jelenti, ahol is egy matematikai állításból képezünk sorozatot. Egy formális matematikai állításban persze olyan szimbólumokat is használni kell, amelyre itt nem tértem ki (∀,ⱻ, ⌐,≡,...).
Nevezetes sorozatok
Természetes számok sorozata: A számosság-generátor sorozathoz rendelt számok sorozata, mint azt már korábban említettük. Érdemes megemlíteni, hogy a sorozattagok, és indexeik (a tagok sorszámai) megegyeznek, vagyis ez a sorozat önmagát indexeli.
Egész számok sorozata: n(i) = i/2 ha i páros, (-i-1)/2 egyébként, i pedig a természetes számok sorozata.
Racionális számok sorozata: r(i,j) = i/j, ahol i az egész számok, j a természetes számok sorozata a kezdőtag (nulla) nélkül. Mint látjuk, itt egymástól függetlenül kétszer is hozzárendeltük a természetes számok sorozatát a racionális számok sorozatához, ami felveti a kérdést, hogy valóban sorozattal van-e ez esetben dolgunk, vagy valami egészen új matematikai struktúráról. Azonban Georg Cantor megmutatta, hogy az átlós bejárással a racionális számok sorozata egyetlen hozzárendeléssel is előállítható, egyetlen sorozatba fűzhető, vagyis valóban sorozat, és számossága ennek megfelelően megszámlálható végtelen.
Számrendszerek: bár már fentebb leírtuk a tízes számrendszer felépítését, ide kívánkozik újbóli megemlítése, hiszen ez is egy általános sorozat, ezen kívül minden egynél nagyobb természetes számhoz rendelhető számrendszer. A gyakorlatban a kettes, hármas, nyolcas, tízes, tizenhatos számrendszerek használata terjedt el, de bármi más is lehetséges. Mivel minden sorozat között ekvivalencia hozható létre, így bármely sorozatot lehet az egyszerű sorozat definíciójának szabályai szerint is definiálni, tehát a kezdőelem, és a rákövetkezési szabály megadásával. Történetesen a tízes számrendszer elterjedése történelmileg megelőzte a többi definíciót, de én a számossággenerátor sorozatból való kiindulást sokkal kifejezőbbnek tartom.
Ezen sorozatok részletesebb tárgyalására itt nem térünk ki, mivel ezek definíciója csak annyiban módosul a hagyományos definíciókhoz képest, hogy a korábbi halmazként kezelés helyett sorozatként kezeljük őket, a természetes számok sorozatából kiindulva. Ezen különbségek persze bizonyos szempontokból nagyon lényegesek.
Egy speciális sorozatról azonban még szólnunk kell, mivel a továbbiakban hivatkozni fogunk rá. Ez a sorozat az f(n) = 1/n. Ennek érdekessége, hogy n növekedésével a tagok egyre kisebbek, és egyre közelebb kerülnek nullához. Bár ez a közeledés szigorúan monoton csökkenő, de a tagok mindig nagyobbak nullánál, és azt soha nem érik el. Nem tudunk olyan kicsi nullánál nagyobb racionális számot mondani, amelyhez ne tudna jobban közeledni nullához ez a sorozat.
Végtelen számosságú halmazok, végtelenszer elvégzendő műveletek
Felmerül a kérdés, hogy vannak-e végtelen számosságú halmazok? Hiszen eddig csak véges számosságú halmazokról, véges számokról, és végtelen sorozatról volt szó. Nyilvánvalóan vannak végtelen számosságú halmazok is, hiszen egy intervallum pontjaihoz is rendelhető halmaz, amely végtelenségig osztható, tehát tartalmazza minden osztalékát, de mindenekelőtt világossá kell válnia, hogy mást jelent egy halmaz számosságának végtelensége, és mást jelent egy sorozat végtelensége. Az intervallum felosztása végtelenségig folytatható, ezért soha be sem fejeződik a felosztás algoritmusa, de mivel az osztalékok mindig az intervallumban maradnak, így a teljes osztalék sorozat is szükségképpen az intervallumban van, hiszen maga az intervallum nem változik a felosztás által. A felosztásban egy intervallumot kettéosztó osztópontot természetesen csak az egyik intervallumhoz tartozónak tekintjük, hogy ne duplázzuk meg az osztópont jelenlétét. A halmazok végtelenségének fogalmának megértéséhez további ismeretekre, és intuícióra van szükségünk a sorozatok tulajdonságaival kapcsolatosan. A korábbiakban definiáltunk olyan számrendszereket, amelyekben véges számú számmal véges számú művelet alkalmazásával jutottunk véges számú eredményhez, amelyek ebből kifolyólag szintén véges nagyságúak. Most elkezdjük vizsgálni a végtelen számú művelet alkalmazhatóságának lehetőségeit, igényeit, mivel az eddig tárgyalt véges aritmetika erre nem alkalmas.
Ehhez egy újabb axiómára lesz szükségünk:
AX4:
, vagy más jelöléssel
1+1+1+... = ∞,
ahol a hozzáadások végén levő három pont (…) az előtte szereplő hozzáadás végtelen sokszori alkalmazását jelenti, a ∞ pedig a végtelent jelölő szimbólum.
Vagyis az egyszerű aritmetikai műveleteknek, mint amilyen a rákövetkezés műveletének megfelelő +1 hozzáadásnak végtelenszer való alkalmazása végtelen nagy mennyiséget hoz létre (Ez a rákövetkezés és az aritmetikai +1 megfeleltetés következménye). Vegyük észre, hogy a 'végtelenszer való alkalmazás' fogalmilag, és tartalmilag is jelentősen különbözik a 'tetszőleges számú alkalmazás' fogalmától, mivel ez utóbbi csak véges számú alkalmazást jelöl, vagyis azt, hogy a rákövetkezés művelete, és az ezekből származtatott aritmetikai műveletek véges számból csak egy másik véges számra juthat, nem vezet ki a természetes számok köréből.
Az új axiómánk következményeként adódik néhány speciális műveleti eredmény:
n + ∞ = ∞,
∞ + ∞ = ∞,
n · ∞ = ∞,
∞ · ∞ = ∞,
n / ∞ = 0,
n / 0 = ±∞,
∞ / ∞ = ?,
∞ - ∞ = ?
(n / ∞) / (m / ∞) = ?.
Ezek persze nem kezelhetők a véges számokra definiált aritmetikai műveletek részeként, hiszen látható, hogy a véges aritmetikában a ∞ szimbólum számként kezelése hibás. Az utolsó három sorban a kérdőjel azt jelzi, hogy az ilyen kifejezések értéke nem meghatározott, akármi is lehet.
Megjegyzendő, hogy gyakran az axiómában szereplő egyeseknél kisebb mennyiségek végtelenszer való összegzése is végtelen eredményt adhat, például a racionális (1, 1/2, 1/3, 1/4, 1/5, 1/6, ...) sorozat tagjainak az összege is végtelen. Bizonyítás: A tagokat zárójelekkel csoportosítsuk: 1+(1/2)+(1/3+1/4)+(1/5+1/6+1/7+1/8)+(1/9+..+1/16)+(1/17+...1/32)+..., tehát a zárójeleken belül rendre kétszer annyi tagot vonunk össze, mint a megelőző összevonásban. Az egyes zárójeleken belüli utolsó legkisebb taggal helyettesítve a többi tagot a zárójeleken belül rendre 1/2 értéket kapunk, ami tehát a helyettesítés miatt kisebb, mint a helyettesítés előtt volt. A végtelen sok (1/2)-et páronként tovább összevonva az axiómában szereplő kifejezésre jutunk. Tehát
, vagy másképpen 1+1/2+1/3+1/4+1/5+1/6+... = ∞.
Ugyanakkor az is könnyen megmutatható, hogy nem minden esetben ad végtelen eredményt egy sorozat tagjainak összege. Például osszuk fel a nulla, és egy közötti intervallumot a racionális 1/2n sorozattal, vagyis rendre felezzük meg a nullához közelebbi intervallumokat. Nyilvánvaló, hogy a teljes hosszúság nem változik, ha az intervallumot felosztom több részre.
[0,1] = [0,...] ∪ ... ∪ (1/16,1/8] ∪ (1/8,1/4] ∪ (1/4,1/2] ∪ (1/2,1]
Az intervallum végét jelző zárójel kerek, ha a végpont nem tartozik az intervallumhoz, és szögletes, ha a végpont az intervallum része. Látható, hogy az intervallumok hosszúságait az 1/2n sorozat adja. És látható, hogy a kapott rész-intervallumok hosszúsága pontosan megfelel a kapott részintervallum nullához közelebbi végének racionális osztópontjával. Vagyis a teljes intervallum hossza nem más mint a felosztott végtelen számú intervallum hosszának összege, ami pedig a racionális sorozat végtelen számosságú tagjainak összege a legelső, nulladik (egy értékű) tag kivételével. Így hát . A sorozatok tagjaiból alkotott végtelen összegeket egyszerűn végtelen sornak nevezzük. Ha a sor összege véges, akkor a sort konvergensnek nevezzük, ellenkező esetben pedig a sor divergens.
A fenti műveleteket, vagyis a sorozat végtelen számosságú tagjának bevonását (nem csak összegzés esetében) valamely matematikai műveletbe, határérték képzésnek nevezzük, az eredményt pedig határértéknek. De a határérték képzés fogalmát a matematikai analízisben más értelmezésben is használják, nem csak sorozatokra vonatkoztatva. Fent az összegzés határát bővítettük ki végtelenre, de ugyanilyen értelemben véges aritmetikai kifejezések végtelenre való kiterjesztésére más jelölést is használhatunk:
Látható, hogy ténylegesen nem végzünk el végtelen számú műveletet, mivel számunkra, a végesben létező lények számára ez lehetetlen, hanem kerülő utakon következtetünk a végeredményre, tehát jelen esetben a végeredmény intervallum felosztásához rendeltünk egy végtelenségig folytatható algoritmust, vagyis egy sorozatot. Ezek a kerülőutak nagyon sokfélék lehetnek, némi intuíciót igényelhetnek, esetleg nem is találunk ilyet, és akkor nem tudjuk meghatározni a határértéket. Néha nem használjuk explicit a határértékképzés szót, miközben ténylegesen határértékképzést végzünk. A fenti példákban például a sorozatok tagjainak összegét egyszerűen sornak nevezzük, és a sor összegeként hivatkozunk a határérték képzés eredményére, miközben csak három pont jelöli az összegek végén, hogy végtelen sok taggal kell számolnunk. Ha nullától végtelenig összegzünk, gyakran elhagyjuk az összegzési határokat, például úgy írjuk: .
Ezek után azt kell látnunk, hogy ha egy sorozat tagjait egy halmazban akarjuk tudni, akkor a tagok halmazainak unióját kell képeznünk, mégpedig végtelenszer. Tehát a számosság-generátor sorozat halmaza:
Ebben a végtelen unió utolsó tagját pontosan az utolsó axiómában szereplő végtelen összeggel fejezhetjük ki, így a halmaz kétségkívül tartalmazza a végtelent, ugyanis pontosan ugyanazon indexelés szerint képezzük az uniót, és képezzük az utolsó tagot:
∅ ∪ ∅+ ∪ … {1+1+1+...} = ∅ ∪ ∅+ ∪ … {∞} = {S} = 𝕀.
Ez az eredmény meglehetősen kényelmetlen következményekkel jár. A halmazba olyan objektum került, amely nem véges természetes szám, és nem érvényes rá a természetes számokra vonatkozó aritmetika, sőt a halmazra az elemi halmazműveletek alkalmazása is kérdésessé vált. Egyedül a rákövetkezés művelete érvényes a végtelen nagy tagra, hiszen az új axióma szerint a végtelen nagy tag rákövetkezője is végtelen nagy. Így nem is egy végtelen tagunk van, hanem a végtelen nagy tagok száma is végtelen. A végtelen nagy tagoknak nincs sem kezdő, sem befejező, nincs sem legkisebb, sem legnagyobb eleme, és közöttük nem definiálható rendezés. Ez egy eddig nem tárgyalt újabb számosság értéket jelent, amit megszámlálhatatlan végtelennek nevezünk, ugyanis a végtelen nagy tagok indexelése nem lehetséges véges indexekkel. Ennek kapcsán felmerül ezen új értéknek a viszonya a korábbi megszámlálható végtelenhez, vajon nagyobb-e nála. Mivel a végtelen halmaz számosságát a sorozatokat magukba foglaló halmazok számosságaként definiáltuk így a halmazokra használt megszámlálhatatlan végtelenre nagyobb számosságként tekintünk, mint a sorozatok számosságára használt megszámlálható végtelenre. Ugyanis a véges indexű tagok felelnek meg a megszámlálható végtelenségnek, és az ennél nagyobb végtelen indexű tagokhoz nem rendelődik véges index, tehát nem feleltethetők meg egymásnak, így egy nagyobb számossággal van dolgunk.
Legalább is a természetes számok sorozatából képezett halmazzal ez a helyzet. De felmerül a kérdés, hogy a korábban vizsgált konvergens sorozatból képzett halmaz esetében mi a helyzet. A sorhoz adott tagok egyre kisebbek, és nyilvánvalónak tűnik, hogy a határértékben megjelenő végtelen nagy indexű tagok már semmit sem adnak hozzá az összeghez, vagyis azonosak. Így ez egyetlen elemet jelent a halmazban, a határérték belekerülését, amely nem ad számosságbeli különbséget a sorozat megszámlálhatóan végtelen számosságához képest. Ezért a konvergens sorozatokból képzett halmazok megszámlálhatóan végtelen számossága megegyezik a sorozat számosságával. Az index halmaz (természetes számok sorozatából képzett halmaz) és a konvergens sorozat halmazának különböző számossága abból is látszik, hogy a végtelen számosságú végtelen nagy indexű tagok, és az egyetlen határérték között nem lehetséges egy-egy értelmű megfeleltetést létrehozni.
Azokat a konvergens sorozatokat, amelyek határértéke nulla, nullsorozatoknak nevezzük, és ezekből megszámlálhatatlanul végtelen sok létezhet, mivel még csak általános megszámlálási elveket sem tudunk megfogalmazni a megszámlálásukra. Ha egy ilyen sorozat minden tagjához hozzáadunk egy tetszőleges számot, úgy a sorozat továbbra is konvergens marad, és ennek a sorozatnak a határértéke ez a hozzáadott szám lesz.
A természetes számok halmaza
A most alkotott 𝕀 halmazzal nagy probléma van. Mivel végtelen nagy számokat is tartalmaz, nem igazán használható, mivel sem az aritmetikai, sem a logikai műveletek nem használhatók a halmaz elemeire. Ezért ha halmazműveletekben akarunk a természetes számokra hivatkozni, akkor egy másik halmazra van szükségünk. Valahogy ki kell zárni a végtelen nagy számokat a halmazból. Ehhez el kell határolni valahogy a véges, és a végtelen nagy számokat. Erre definiálunk egy szimbólumot, és adunk hozzá egy újabb axiómát.
Jelentsen a ≺∞ szimbólum egy olyan véges számot, amely nagyobb minden véges számnál, de kisebb minden végtelen nagy számnál. Ez a szám közelebbről nem meghatározható, de így is nagy jelentősége van. Nevezhetjük a véges számok horizontjának. Az új axióma:
AX5: ≺∞ alkalommal összegezve az egyet, az ≺∞ értéket ad eredményül. .
Ezzel a határérték képzés új részleges módját vezethetjük be, amely az összes véges tagot figyelembe veszi, de a torlódási pontot, vagy pontokat nem adja hozzá. Ez megfelel annak az ismert szemléletnek, amely egy adott pont környezetét tekinti, de az adott pontot nem. Tehát például , vagyis ez a határérték a 1-nél kisebb szomszédos racionális számot adja eredményül.
Így a természetes számok hagyományos halmaza = ℕ.
Hasonló módon az egész számok sorozatának uniójából részleges határértékkel képezhetjük az egész számok ℤ halmazát, és a racionális számok sorozatának uniójából részleges határértékkel képezhetjük a racionális számok ℚ halmazát.
Valós számok halmaza
Eddig bár említettük az intervallum fogalmát, és annak felosztását véges számú aritmetikai művelettel, de nem vizsgáltuk, hogy vajon ezzel a racionális felosztással minden intervallumbeli szám előállítható-e. Már az ókori püthagoreusok rájöttek arra, hogy egy négyzet, és átlója között nincs racionális arányosság, vagyis az egységnyi oldalú négyzet átlójának hossza nem lehet racionális szám. Ennek bizonyítása elég egyszerű, felhasználva a Pitagorasz tételét. E szerint az a oldalú, a*c átlójú négyzetre a2 + a2 = a2*c2. Ebből c2 = 2. Tételezzük fel, hogy c egy racionális szám, vagyis felírható r/s alakban úgy, hogy ne legyen mindkettő páros. c2 = (r/s)2 = 2, átrendezve r2 = 2 s2. Mivel a jobb oldalon páros szám áll a kettővel való szorzás miatt, így a bal oldalon is páros számnak kell lennie. Csak hogy mivel a baloldalon négyzeten szerepel ez a páros szám, így az már néggyel is osztható. De a baloldal csak akkor osztható néggyel, ha s2 is páros, ami ellenkezik azon feltevésünkkel, hogy csak az egyik szám páros. Ezért c nem lehet racionális szám. Viszonylag könnyű olyan algoritmust tervezni, ami olyan racionális sorozat tagjait állítja elő, amelyik tetszőlegesen megközelítheti ezt a c számot, vagyis a határértéke c. A c számot irracionális számnak nevezzük. De nem csak egyetlen ilyen irracionális szám van. Könnyen belátható, hogy bármely két (különböző) racionális szám között végtelen sok racionális, és irracionális szám van. Ez két állítás. Az első bizonyítására elég figyelembe venni, hogy két különböző racionális szám számtani közepe is racionális, és különbözik mindkét racionális számtól, valamint, hogy ez a számtani közép képzés végtelen sorozatban folytatható. A végtelen sok irracionális létezéséhez azt kell látni, hogy míg a számtani közép képzések racionális sorozatok tagjait képezik, ezen sorozatok határértékei is megszámlálhatatlan végtelenre szaporodnak. Bármikor felfüggesztjük ezen sorozatok képzését valamely véges indexnél, úgy véges felosztást kapunk, bármely véges indexre racionális, megszámlálhatóan végtelen sorozatról beszélhetünk, de ezen sorozatok határértékei tartalmazzák a megszámlálhatatlan végtelen irracionális számokat. A racionális számok, és irracionális számok összességét valós számoknak nevezzük. A korábban már használt intervallum alatt a valós számok összefüggő tartományát értjük. Praktikusan a valós számok halmaza nagyon hasonlóan állítható elő mint az előző szakaszban a racionális számok halmaza, de részleges határértékképzés helyett teljes határértékképzést használunk.
Végtelen halmazok
A végtelen számosságú halmazok fogalmának bevezetése miatt a cikk elején a véges halmazokra definiált halmazműveletek ki kell terjeszteni a végtelen esetekre is, aminek nincs különösebb akadálya. Azonban nem szabad elfelejteni, hogy ha egy végtelen számosságú halmaz minden elemét felhasználjuk valamely műveletben (ΠΣ∪∩), az csak a határértékképzéssel tehető meg, akár explicit, akár implicit módon tesszük. És ez a konvergens sorozatok (vagy azokból alkotott halmazok) kivételével megszámlálhatatlanul végtelen elemet jelent. Ez a tulajdonság különösen fontossá válik a természetes számok (divergens) sorozatát tartalmazó halmazok számára.
A számosság fogalmához definiáltuk a számosság-generátor sorozatot. Ez előállította az összes véges számosságú halmazt reprezentáló halmazokat, amelyekhez a természetes számok fogalmát is rendeltük. Véges számosságú halmazokból megszámlálhatóan végtelen van, és ez egy újabb számossági fogalom, amelyhez még a továbbiakban a divergens sorozatokat tartalmazó halmazok megszámlálhatatlan végtelensége járult. Georg Cantor a róla elnevezett tételben bebizonyított, hogy bármely halmaz hatványhalmaza nagyobb számosságú, mint a halmaz. Ezt a tételt nehéz megcáfolni, de eddig nem sikerült reprezentálni olyan halmazt, amely a valós számokénál nagyobb számosságú. Ugyancsak Cantor azt is bebizonyította, hogy a véges több dimenziós terek nem képviselnek nagyobb számosságot, mint az egydimenziósak. Ahol a számosság növekedése mégis előfordulhat, az esetleg a végtelen dimenziós terek számossága lehet.
Korábbi hibás állításokról.
Sorozatokkal, vagy sorozatok tagjaival műveleteket végezhetünk, amelyet két fő csoportba oszthatunk.
1. Egy vagy több sorozat kiválasztott tagjaiból, valamely műveletek által egy új sorozatot képezünk. A műveletek eredménye tehát egy másik sorozat, amelynek tagjai szinte tetszőleges matematikai objektumok lehetnek (számok, halmazok, sorozatok). A hagyományos matematika ezt használja a sorozat definíciójaként, de valójában csak sorozatok közötti leképezésről van szó, amely konkrét sorozatokat nyilvánvalóan definiálhat, de a sorozat fogalmát nem érinti, amelyet a természetes számok sorozatának axiómái definiálnak.
2. Egy vagy több sorozat összes tagja képez valamely műveletek határértéke által véges sok számot, halmazt, vagy megszámlálhatatlan számosságú halmazt.
Hatványhalmaz fogalma: Egy A halmaz minden lehetséges részhalmazának halmazát hatványhalmaznak nevezzük, jelöljük most: H(A).
H(A) = { X | X ⊆ A }. Csak halmazhoz rendelhető hatványhalmaz, sorozathoz nem.
Véges n számosságú A halmaz hatványhalmazának számossága 2n, vagyis minden újabb elem az alaphalmazban megkétszerezi a hatványhalmaz számosságát. Véges számosságú halmaznak a hatványhalmaza is véges számosságú.
De mi van a megszámlálhatatlan végtelen számosságú halmazokkal? Egyrészről nem konstruálható meg egy ilyen halmaz hatványhalmaza, mivel meg sem számlálható. Ha egy halmaz nem számlálható meg, akkor nem létezik olyan függvény, amely a halmazt elemeire elkülöníthetné, és ez esetben az elemeinek minden lehetséges részhalmaza sem hozható létre. De a hatványhalmaz definíciója nem érinti ezt a problémát, és a Cantor tétel bizonyítása sem.
De mi van a sorozatokkal? Azokhoz rendelhető hatványsorozat, amelyben a sorozat tagokat jelentő részhalmazok számossága minden alapsorozati tag hozzá vételével megkétszereződik, vagyis követi a véges esetek logikáját. Vagyis a megszámlálhatóan végtelen számosságú sorozatok hatványsorozatainak számossága is megszámlálhatóan végtelen. A megkétszereződésből következően adódik egy kézenfekvő egy-egy értelmű megfeleltetés a kettes számrendszerben felírt számok helyi-értékeinek sorszáma, és a természetes számok között, ahol az adott helyi-értéken álló egyes az adott szám szerepeltetését jelenti a részhalmazban. Nevezzük ezt helyi-érték megfeleltetés függvénynek, megjegyezve, hogy ha külön nem említjük, akkor a kettes számrendszerben felírt szám helyi-értékeiről van szó.
De mi van a konvergens sorozatokat tartalmazó halmazokkal? Az ilyen halmazokhoz legelső előtti elemként (-1 indexszel) hozzá kell venni még egy elemet, ami a határértéket tartalmazza, és mivel így ez a halmaz sorozatként kezelhető, a sorozatokhoz hasonlatosan kell képezni a hatványsorozatát.
A leggyakoribb ellenvetés éppen annak a meg nem értésén alapul, hogy sokan nem szokták meg, vagy nem is ismerik a különbségtételt a hatványhalmaz, és a hatványsorozat fogalma között. A hatványhalmazt halmazhoz definiáljuk, a hatványsorozatot sorozathoz. Sorozathoz csak sorozat rendelhető egy-egy értelműen, úgy hogy minden egyes sorozat taghoz rendelünk egy-egy értelműen valami más dolgot, például a tag hatványhalmazát. Sorozaton értelmetlen a hatványhalmaz fogalmát értelmezni, mivel más a sorozat, és más a halmaz definíciója, nem értelmezhető közöttük egy-egy értelmű megfeleltetés.
Amikor a Russell paradoxon, és más logikai paradoxonok léte napvilágra került, sok matematikus gondolta, hogy a naiv halmazelmélet tarthatatlan, mert ilyen paradoxonok felléphetnek benne, és rögvest seregnyi új axiomatikus megközelítést publikáltak, amelyek némelyike meg is gyökeresedet a matematikában. De ezekkel két súlyos probléma van. Ez egyik, hogy nem vették észre a sorozatok halmazként való kezelésének logikai hibáját, így maguk is hibásak. Másrészt pedig nem vették figyelembe a Gödel tételek eredményeit, vagyis minden alapot nélkülözött az a korábbi elvárásuk, hogy az axiómákkal, és definíciókkal zárják ki a paradoxonok, és ellentmondó állítások meglétét. A matematika is egy nyelv, akárcsak a beszélt nyelvek, és nincs, nem lehetséges létrehozni olyan értelmes nyelvet, amelyben ne lehessen hazudni. A nyelv nem a gondolkodás helyettesítésére való, hanem a gondolatok kifejezésére.
Végtelen nagy egész számok
Hogyan értsük, hogy a korábbi cikkeim szerint a véges természetes számok halmaza nyílt halmaz?
Tekintsük az 1/n sorozatot, és a tagokból képezett halmazt. A függvényértékek n növekedésével egyre jobban közelítenek a nullához. Ha a sorozat részleges határértékét vesszük, akkor a nulla nem szerepel a függvényértékek között, azok a ( 0, 1 ] nyílt halmazból kerülnek ki. Ha a teljes határértéket vesszük úgy az értékkészlet a nulla értéket is felveszi, vagyis a [ 0, 1] zárt intervallumból kerülnek ki.
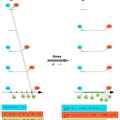
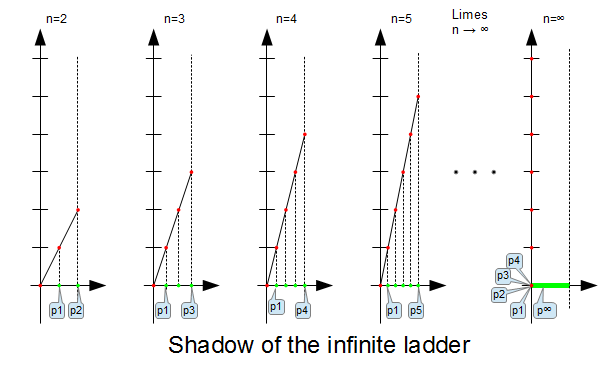
Milyen arányban van a véges, és a végtelen nagy számok számossága? A végtelen létra árnyéka szemlélteti ezt a legjobban, amely a Peano-görbe egydimenziós vetületeként is felfogható. Az ábrán jól megfigyelhető az index sorozat, és a vetület halmaz közötti leképezés, illetve, hogy ez hogyan módosul a határértékben.
Ismeretes, hogy nevezetes irracionális konstansokat csak racionális közelítő számokként tudunk meghatározni, vagyis két természetes szám hányadosaiként. Minél pontosabb a közelítés, annál nagyobbak ezek a természetes számok. A keresett irracionális számot ezen sorozatok határértéke jelenti, tehát az irracionális számokat két végtelen nagy egész hányadosaiként is értelmezhetjük. Ezek persze nem egyértelműen meghatározottak, mivel bármely tört tetszőlegesen bővíthető.
A korábban említett helyi-érték megfeleltetés függvény végtelen számokra való kiterjesztésével gyakorlatilag bármely egész értékű sorozat értékkészletéhez megfeleltethetünk egy egyértelműen meghatározott végtelen nagy számot. Így a páros számokhoz, a páratlan számokhoz, a négyzetszámokhoz, a prímszámokhoz is egy-egy meghatározott végtelen nagy szám tartozik, amelyek minden véges helyi-értékű számjegye meghatározott. A helyi-érték megfeleltetés függvény tehát kiterjeszthető, a végtelen számok bináris felírását feleltethetjük meg az egész számok részhalmazainak, sorozatainak.
A végtelen számok a matematikában ezelőtt is ismertek voltak, több mint száz éve, mint a p-adikus számok egyik formája, és amelyeknek másik formái a racionális számok. A p-adikus számok persze csak a periodikusan felírható végtelen számokat fedik le valamely p prím szám alapú számrendszer szerint. A végtelen számoknak ez a része tehát megszámlálható számosságú, szemben a nem periodikus végtelen számokkal.
Lényegi különbségek a korábban elterjedt elméletektől
A számok szokásos definíciói további axiómákat is tartalmaznak az itt szereplőkhöz képest, miszerint létezik a természetes számokat tartalmazó halmaz (ZF, ZFC axiómarendszerek, végtelenségi axiómája). Ezt axiómaként kimondva, fel sem merült sokakban a kérdés, hogy ez esetleg egy logikailag hiányos axióma, hiszen az axiómát nem kell bizonyítani, így mindenki felmentve érzi magát az axióma rendszer konzisztenciájának bizonyítását illetően. Mint fent láttuk, sok olyan halmaz létezhet, amely tartalmazza a véges természetes számokat, csakhogy ezek a halmazok vagy másféle objektumokat is tartalmaznak, mint például a végtelen nagy számok, vagy olyan nyílt halmaz, amelynek komplementerhalmaza nem üres. Valójában ez az axióma így teljesen fölösleges, hiszen a rákövetkezés művelete önmagában képes meghatározni, hogy milyen halmazok tudják tartalmazni a természetes számokat, lévén egy egyértelműen meghatározott sorozat egyértelműen meghatározza a határértékét is (amennyiben az létezik), másrészt egy hibás elképzelést sugallt a természetes számokról. A hagyományos matematika képtelen megkülönböztetni a sorozat, és a sorozatot tartalmazó halmaz fogalmát, természetellenesen, és logikailag hibásan azonosnak veszi ezen két gyökeresen különböző (különbözőképen létrehozott) objektumot, így nem is képes számot adni különbözőségükről.
Mivel az említett axióma rendszerek a jelenlegi matematika alapozásai, így eredendő hibájuk minden jelenlegi matematikai állításra kiterjed, vagy kiterjedhet. Axióma mivoltuk miatt nem érvényesek rá a matematikai bizonyítások szabályai, mivel bizonyítani sem kell az axiómákat, így persze cáfolni sem lehet őket szabályos matematikai bizonyítással. Ezért a hiba kimutatása is csak egy alternatív axiomatikus felépítésen keresztül lehetséges, ami így már jóval átfogóbb terjedelmű, mint egy hibás tétel hibájának bizonyítása. Sajnos a matematikusok manapság a valóságtól elrugaszkodva, teljesen független állításként értelmezik az axiómák fogalmát, így képtelenné váltak annak megértésére, hogy mi a kapcsolat a matematika, és a valóság között. Pedig ez Euklidesz óta ismert. Az axióma olyan egyszerű állítás, amelynek igazságtartalma annyira nyilvánvaló, és magától értetődő, hogy nincs igényünk igazságtartalmának bizonyítására, mivel igazság tartalmukkal kapcsolatosan semmilyen kétségünk nem marad. Nem véletlen, hogy amikor több mint másfél ezer év után kétség merült fel Euklidesz egyik axiómáját illetően, annak egyetemes értelmezését el is vetették. Ugyanezen az alapon a most említett végtelenségi axiómának meg sem szabadott volna születnie, mivel a sorozatok definiálása nem azonos a halmazok definiálásával, és ennek axiomatikus azonosítása nem magától értetődő, sőt, mint az itt olvasható, hibás.
Hibás a sorozat szokásos definíciója is, mely szerint "a sorozat a természetes számok halmazán értelmezett függvény". A feje tetejére van itt állítva a logika. A matematikai bizonyítások alapját adó teljes indukció elvének sorozatokban megnyilvánuló axiomatikus rögzítése helyett egy zavaros halmazaxiómára építik a sorozatokat, és így az indukciót.
A későbbiekben újabb axióma rendszerek születtek a természetes számokról, de ezen a problémán ezek sem tették túl magukat, ezzel szemben olyan akadémikus szintre emelték a matematika legelemibb alapjait, amely gyakorlatilag húzza ki a talajt a matematika alól. Ezzel a matematika a tudományok szilárd megalapozása helyett elvont spiritiszta elmélkedéssé vált.
A halmazok szokásos definíciója axiómaként mondja ki a hatványhalmazok létezését. Ez szintén durva hiba, hiszen az egy egyszerű következmény, hogy egy halmaz elemeiből hogyan lehet részhalmazokat képezni a definiált halmazműveletek segítségével, és létezhet-e az összes lehetséges részhalmaz halmaza. Ráadásul egy kontinuum számosságú halmazhoz senki sem tud konstruálni hatványhalmazt, éppen azért nem, mert elemei megszámlálhatatlanok, így eleve kétséges, hogy létezőnek tekinthető egy ilyen hatványhalmaz egy adott műveletben, vagy sem, és az csak mint feltételezés tárgyalható.
Az itt használt ún. naiv halmazelmélet bőségesen elegendő a matematika egzakt tárgyalására. A későbbiekben a naiv halmazelméletet olyan igényekkel vetették el, amelyeket később sem sikerült beteljesíteni, sőt bizonyossá vált, hogy ez az igény nem is teljesíthető. Ez volt az új axióma rendszerek bevezetésének másik oka, amely megint csak elbonyolított olyan dolgokat, amiknek a lehető legegyszerűbbeknek kell lennie, ahogyan azt Euklidesz óta tudjuk. Az axiómák akadémikus bonyolultsága az egyik eredendő oka annak, hogy a matematika legelemibb alapjaiban bizonytalanságok, és rejtelmek vannak.