Although the terms defined here are similar to those of the same name as defined elsewhere, they are often not identical to it, and there are even significant differences, so we need to be careful about the environment in which we use it, because in other environments there may be gross errors and misunderstandings. The purpose of the brief description is precisely to make these ideas comparable to those common elsewhere. However, I will not address many of the issues that are well known or familiar from the usual way of negotiating. (This translation relies heavily on Google's help, so if something is meaningless, the Hungarian version can help you understand.)

Basic concepts

Since this article deals only about the interpretation of sets, cardinalities, and natural numbers, there will be no definitions of preliminary mathematical concepts in some other areas, I assume they are known in advance. These are basic knowledge of mathematical logic, mathematical statements, and relations, concepts of mappings, and one-to-one mappings. These are largely refined formulations of the logic of ordinary language, and I myself do not wish to delve deeper into their application, so perhaps no more serious preliminary study is needed to make my writing comprehensible to anyone. I will introduce new mathematical concepts gradually, preferably making sure that I discuss only the simpler knowledge first, and only then, relying on it, to get to the more complex knowledge. Because of this, as we will see, certain mathematical structures will also have simpler, and more complex, more complete versions. This step-by-step, increasingly in-depth way of negotiating the expansion of knowledge can also be traced back to deeper philosophical considerations, since only in this step-by-step way can we build our knowledge in a logically correct way, whether mathematically or otherwise. Current axiom systems want to define everything in their full depth in one step, and therefore the foundation of the theory becomes opaque, uncontrollably complicated. As they say, whoever grabs a lot will take a little.

Definition of the finite set

A set is an arbitrary group of objects in which each distinguishable object is called the elements of the set. The set is clearly defined by its elements, and vice versa; the set clearly defines its elements. A group in which the affiliation of objects cannot be clearly defined cannot be called a set. Objects whose affiliation cannot be unambiguously determined do not form a set. We can encounter paradoxical set definitions that lead to a contradiction regarding elemens, i.e. from contains comes the demand for non-contains, and from non-contains comes the demand for contains. These are incorrect logical definitions, and sets defined in this way cannot logically exist. Therefore, the clarity of the definition of belonging to a set is a necessary condition for the existence of a set. Objects selected in a set become a set because we selected them, that is, a set is a purely abstract concept, the elements of which can be either physically existing things, or even the elements can be abstract concepts also. The elements of the set must be different from each other. Mathematical structures similar to a set in which identical elements can occur more than once are not called sets but multisets, and are discussed at a higher level by mathematics, not discussed in this paper, only for the sake of completeness it seemed necessary to mention here the reason for this narrowing. By not allowing element identity in a set, it represents a significant simplification in the future, which makes it easier to learn the theory of sets. In other respects, the objects that make up the set can be anything. Objects, concepts, anything. In the description, anyone can recognize the so-called based on naive set theory, but we start with only sets containing a finite number of elements. The set theory can be extended only if the necessary concepts (infinite) have been defined. By way of example, if we stack pebbles next to each other to form a set, we assume (otherwise quite rightly) that no two pebbles are the same and only a finite number of pebbles are available to us.

Markings

Let H be a set whose elements are a, b, c, and d.
This is denoted by H = {a, b, c, d}.

Thus we denote that a element of the set H is: a ∈ H

There is a universal special set, the empty set {} = ∅, which contains no element. Universal, because if we remove its elements from any set containing objects, we get the same empty set.

Subset: A ⊆ B, every element of set A is also an element of set B.

Real subset: A ⊂ B, every element of set A is also an element of set B, but not all elements of set B are elements of set A.

The elements of a set can themselves be sets.

For example, C = {{}, {{}}, {{}, {{}}}} is also a set, but its elements are merely different sets formed from an empty set, that is, a purely mathematical abstraction based on the properties of the set defined here.

Operations

Set fusion or union: {a, b, c, d} ∪ {c, d, e, f} = {a, b, c, d, e, f}

Common part or section: {a, b, c, d} ∩ {c, d, e, f} = {c, d}

Difference or subtraction or removal: {a, b, c, d} \ {c, d} = {a, b}

These operations clearly show that the elements with the same designation are one and the same element.

On the cardinality of finite sets:

If a one-to-one correspondence can be established between the elements of two sets for all the elements of both sets, then the two sets have the same cardinality. If such a match affects only all the elements of one set, while only a part of the elements of the other set, then the other set is more cardinality and one is less cardinality. The real subset is smaller cardinality. There is no smaller cardinality than the cardinality of empty sets, which is also the set with the smallest number. Sets of the same cardinality define an equivalence class, ie the sets can be classified into equivalence classes according to their number of elements. Based on the smaller or larger cardinality, we can interpret sorting on the equivalence classes. We often return to the concept of cardinality.

Definition of the simple infinite series:

The simple infinite series is a complex mathematical object that has members. Among the members is a distinguished member called the starting member. In the simple infinite series, we define a succession rule that, based on the members already defined, defines a subsequent member for any member that cannot be the same as any previously defined member. In simpler cases, we can specify a sequence by listing the first few members and ... if it does not cause a misunderstanding (0,2,4,6, ...), or (1,2,4,8, ...) . The succession rule thus defines a new member different from the previous ones for each already defined member, so that a simple infinite sequence cannot have an end, only a beginning and a continuation. That is why we call it infinite. Thus, in the case of the gravel set given as an example earlier, we assume that there is no theoretical limitation to adding newer and different gravel to the gravel set, which is of course only imaginable, unrealistic in reality, and we record exactly the order in which the gravel was placed pebbles in the set. Arbitrary, defined members of a simple infinite series can form a finite set called subsets of members. A subset that includes the starting member and all members up to and including the starting member up to a given member is called the starting slice set assigned to that member in the simple series. The next member for that member is no longer an element of this starting slice set. The starting slice subsets are finite cardinalitity. Since the elements of finite sets can be anything as before if their definition is clear, there can be no other restriction on the members of a simple infinite series, so they can be anything if they are clearly defined by the succession rule. The "simple" clause is included so that there is no need to deal with specific exceptions or the concept of a "general" series to be clarified later. Let us then consider an important specific simple series.

Axioms of the cardinality-generator series S:

1. The members of the series S are sets.
2. Let the starting set of the series S be the empty set. {} = ∅.
3. Each member s has a subsequent s+ member that is different from the member s by adding a new element, and this new element is the set containing the member s: s+ = s ∪ {s}
   

The basic axioms of the science of mathematics must meet special conditions that ensure that mathematics provides a solid foundation for learning about all other sciences, and thus reality. Therefore, these definitions should be taken for granted without leaving the slightest doubt as to their truthfulness. All other complicated and abstract mathematical statements are later derived step by step based on the truth of the axioms, but we can no longer trace the axioms back to even simpler statements, so they must be simple and self-evident. Nevertheless, the same definition can often be formulated in alternative ways, but this does not change the substance. Of course, even an understanding of the basic axioms presupposes some level of knowledge of our world, the spoken language, and the ability of abstraction on which to build further abstractions.

Consequences:

1. ∅ ∈ S ∧ a ∈ S → a ∪ {a} ∈ S.
   
2. Some members from the beginning:
   {},
   {{}},
   {{}, {{}}},
   {{}, {{}}, {{}, {{}}}},
   …
   As you can see, the cardinality generator series is a simple infinite series that is an abstraction based only on mathematical concepts.
3. Using the standard (,, ...) notation for the series: S = ({}, {{}}, {{}, {{}}}, {{}, {{}}, {{}, {{} }}},…)
4. Alternative definition: each subsequent series member is the same as the set formed from the previous series members (i.e., the starting slice). This replaces both the 2nd and 3rd axioms, since the first term is also true, since the series preceding the first term is nothing, so the set formed from it is the empty set. 
5. Each member contains one more element than the previous member. 
6. Each member is different. 
7. Each member is a finite cardinality set.
8. The series has no end, the process of axiom 3 can be continued for any length of time, i.e. the series S is infinite. 
9. The cardinality of each a members is less than the cardinality of following a+ members.  
10. The cardinality of any finite set is equal to the cardinality of a member of the series S. Any theorem here means not only mathematical objects, but also sets of finite numbers formed from arbitrary elements and concepts of our world. Thus mathematics becomes the language of the description of the laws of nature.
11. The series S contains the all cardinality as any finite set. That is, the cardinality of any finite set can be characterized by some member of the series S. Cardinality refers to equivalence classes between sets of the same cardinality, and also defines an order for these equivalence classes in the order of the members of the series S. 
12. There is no member whose cardinality is equal to the cardinality of the series S, since the cardinality of the series S is infinite, but all the members of S are finite. 
13. A mathematical object called a number can be assigned to each member set of the S series in a sense that is also identical to the cardinality of the member set. This assignment defines a series of finite natural numbers. Notice that I defined natural numbers as a series and not as a set, as has been prevalent since the work of Georg Cantor and has survived in subsequent axiom systems! In the current new system of axioms, the notion of infinity is included here in the notions of mathematics through the infinity of series, as a synonym for the notion of any optional finite case. Each finite natural number is uniquely assigned a finite cardinality set, the number of which also characterizes the assigned natural number, and the axiom of succession connects the natural numbers as members of a series. The cardinality of the starting member of the series S, the empty set, and the assigned natural number are zero, and the natural number assigned to each subsequent member is greater than the previous natural number, that is, the order is also interpreted on the natural numbers. In addition to these, the numbers can be used to interpret arithmetic operations starting from the operation of succession, it is possible to interpret their number systems, which help to distinguish them by using some symbols in a certain way, which I will discuss in the next section although they are independent of what I have to say. The axioms presented here are similar to Neumann's model of natural numbers, they may be reminiscent, but according to a different logical structure and conclusions. Although the cardinality generator series S is equivalent to the series of natural numbers, it is not identical with it, mainly for the purpose of conceptually separating the two series, but also to give them each other, thus reminding us that each natural number is a conceptual set of classes of given numbers. abstraction. This association and abstraction is historically and epistemologically the same as the development of the concept of numbers. Separating the two concepts allows us to treat natural numbers as a simple infinite sequence whose members are not sets, only symbols following the rules of number description, or other symbolic notations. But note that the symbols of numbers are actually abstractions of given cardinality sets.
14. Definitions of the N series of natural numbers in the decimal number system: Let the set of digit symbols be {0,1,2,3,4,5,6,7,8,9} or with the words {zero, one, two, three, four, five, six, seven, eight , nine}. The elements of this set are assigned to the plurality generator S series as follows.
    ∅ ↔ 0, that is, the first natural number is 0.
    ∅⁺ ↔ 1, that is, the next natural number is one,
    (s ↔ n) → (s ⁺ ↔ n + 1), that is, the succession operation corresponds to the +1 operation, that is, the addition of each number, and s is a member of the sequence S of the plurality generator, n is a member of the sequence N of natural numbers.
    0 + 1 = 1, 1 + 1 = 2, 2 + 1 = 3, 3 + 1 = 4, 4 + 1 = 5, 5 + 1 = 6, 6 + 1 = 7, 7 + 1 = 8, 8+ 1 = 9, which is the order of the one-digit numbers. Additional numbers are marked by writing several digits in a row according to certain rules. On the right is the smallest place value at which one changes with each addition of digits. If this digit is 9, the next number on the right is 0, while the one to the left of the placeholder is 1, but if there is already a digit, we increase it by one. the ticket as if the number on the right is not taken into account. That is, after the ninth, there is always a transfer to the next locale (left). The introductory numbers of the new local values and their names are 10 ten, 100 hundred, 1000 thousand, 10,000 ten thousand, 100,000 hundred thousand, 1,000,000 one million, 10,000,000 tens of millions, respectively. it can be defined with or without the plurality generator series. Similarly, other number systems can be defined based on a different number of symbols, and such number systems are often used in computer science and number theory. These definitions are equivalent to each other, i.e., each defines a series of natural numbers in the same way, but the definition of the plurality-generator series best shows the abstraction inherent in the number concept. 
    
    The + sign has so far only been used in connection with the addition of 1, but it is also the sign of addition, which is more generally defined as: x + (y + 1) = (x + y) +1, ie the sum of the next number of another number is equal to the sum with the following. From this, important rules for addition can be derived, such as a + b = b + a (commutativity) or (a + b) + c = a + (b + c) (associativity). We also interpret the operation of multiplication in a series of natural numbers: x · (y + 1) = (x · y) + y, that is, multiplying one number by the next of another number, we get the sum of the other number. Similar rules can be deduced here as well. a · b = b · c (commutivity), (a · b) · c = a · (b · c) (associativity). Furthermore, for the inclusion of both operations (a + b) · c = (a · c) + (b · c) = a · c + b · c (distribution or highlighting). In the end, we applied the rule specified for the order in which the operations were performed (multiplication is performed before summation), so that the parentheses could be omitted. Of course, the definitions provided herein can be given in a number of other alternative ways that can be found elsewhere. These are the definitions of the basic arithmetic operations on natural numbers that we can use to calculate. Additional operations are usually defined, such as comparison, subtraction, residual division, residual training, exponentiation, and so on, but these are not discussed here. But to add certain members of a series, we often use the sum summation sign, for example
    , or
    
    
15. If the description of the number systems is defined, the description of the series S is simplified:
    0 = {},
    1 = {0},
    2 = {0,1},
    3 = {0,1,2},
    ...,
    n+ = {0,1,2, ..., n},  or with other designations
    
    ... 
     
    
16. The series defined here form the basis of mathematical number theory. The regular succession of members makes the various statements of number theory transferable to the whole series of natural numbers, that is, to all natural numbers. The best known form of proof in number theory is total induction, in which we prove a statement for a given natural number and then, assuming that the statement is true for any number, we also prove that the statement remains true for the next natural number. Total induction is also the basis for the definition of a simple series as well as the consequences listed. The principle of total induction, and the above axioms are therefore equivalent, there is no need to state another axiom for the principle of total induction to apply. Thus, number theory statements refer to finite natural numbers and use a finite number of natural numbers in the proofs, it may be good, it is not defined, and it is not even possible to determine what and how many finite number is, since their cardinality is not finite. 

General definition of the series

Function values assigned to members of a series of natural numbers by a function are called a series. As we have seen above, the sequence of natural numbers was also obtained as a result of a one-to-one assignment to the sequence of generators, so we could even refer to the sequence of generators here, but the more traditional definition of references to natural numbers is equally appropriate clear. Based on the sequence of natural numbers, we call the members of the series consecutive. The cardinality of sets of values ​​in a series is either countable infinite or finite. Finite cardinality can only be called series because of the indexing that makes the members unique, leaving the indexing no longer series, but only finite cardinality sets. Each complete induction proof also means the definition of a series, and the proof of the correctness of the definition, where we form a series from a mathematical statement. In a formal mathematical statement, of course, symbols that I have not covered here (∀, ⱻ, ⌐, ≡, ...) must also be used.

Notable series

Natural Number Sequence: A sequence of numbers assigned to a cardinality generator sequence, as mentioned earlier. It is worth mentioning that the series members and their indexes (the serial numbers of the members) are the same, i.e. this series indexes itself. 

A sequence of integers: n (i) = i / 2 if i is even,  (-i-1) / 2 anyway, and i is a member of sequence of natural numbers.

Sequence of rational numbers: r (i, j) = i / j, where i is a member of sequence of integer, j is a member of sequence of natural numbers without the initial member (zero). As we can see, here we have independently assigned a series of natural numbers twice to a series of rational numbers, which raises the question of whether we are really dealing with a series in this case, or of some completely new mathematical structure. However, Georg Cantor has shown that with diagonal traversal a series of rational numbers can be produced by a single assignment, concatenated into a single series, that is, it is indeed a series, and its cardinality can be counted infinitely.

Number systems: although we have already described the structure of the decimal number system above, it wishes to be mentioned again here, as it is also a general series, in addition to which a number system can be assigned to any natural number greater than one. In practice, the use of double, triple, octal, decimal, and hexadecimal number systems is widespread, but anything else is possible. Since equivalence can be established between all series, any series can be defined according to the rules of the definition of a simple series, i.e. by specifying the starting element and the rule of derivation. Coincidentally, the spread of the decimal number system has historically preceded other definitions, but I find the starting point of the plurality generator series much more expressive.

Infinite sets, Operations to be performed infinitely

The question arises as to whether there are infinitely cardinality sets? After all, so far we have only been talking about finite cardinality sets, finite numbers, and infinite series. Obviously, there are also infinity cardinality sets, since a set can also be assigned to the points of an interval that is infinitely divisible and obviously contains all its dividends, but above all it must become clear that the infinity cardilaity of the sets and the infinity cardionality of a series are different. The division of the interval can be continued indefinitely, so the division algorithm never ends, but since the dividends always remain in the interval, the entire dividend series is necessarily in the interval, since the interval itself does not change by the division. In a division, a division point that bisects an interval is, of course, considered to belong to only one interval, so as not to duplicate the presence of the division point. To understand the concept of infinity of sets, we need more knowledge and intuition about the properties of series. We have previously defined number systems in which a finite number of operations are obtained using a finite number of operations, which are therefore also of finite magnitude. Now we start to study the possibilities and needs of the applicability of an infinite number of operations, because the finite arithmetic discussed so far is not suitable for this.

To do this, we will need a new axiom:

or with other designations 1+1+1+... = ∞,
where the three dots (…) at the end of the additions represent the infinite multiple application of the addition, and ∞ is the infinite symbol.

That is, applying infinitely many simple arithmetic operations, such as the +1 addition corresponding to the succession operation, creates an infinitely large value (This is a consequence of the arithmetic and arithmetic +1 matching). Note that ‘infinite application’ differs significantly conceptually and substantively from the concept of ‘arbitrary number of applications’, since the latter refers only to a finite number of applications, i.e., that the operation of succession and the arithmetic operations derived from them are finite. you can only get another finite number, it does not lead you out of the circle of natural numbers.

As a consequence of our new axiom, there are some special operational results:
n + ∞ = ∞,
∞ + ∞ = ∞,
n · ∞ = ∞,
∞ · ∞ = ∞,
n / ∞ = 0,
n / 0 = ±∞,
∞ / ∞ = ?,
∞ - ∞ = ?
(n / ∞) / (m / ∞) = ?.
Of course, these cannot be treated as part of arithmetic operations defined on finite numbers, since it can be seen that in finite arithmetic the treatment of the symbol ∞ as a number is incorrect. In the last three lines, a question mark indicates that the value of such terms is not specified, whatever it may be.

It should be noted that often the summation of quantities smaller than some in the axiom can give infinite results, for example, for the members of the rational (1, 1/2, 1/3, 1/4, 1/5, 1/6, ...) series. the amount is also infinite. Proof: Group members in parentheses: 1+ (1/2) + (1/3 + 1/4) + (1/5 + 1/6 + 1/7 + 1/8) + (1/9 + .. +1/16) + (1/17 + ... 1/32) + ..., so we enclose twice as many members in parentheses as in the previous merge. Substituting the last smallest term within each parenthesis gives the other terms within parentheses a value of 1/2, which is less than before the substitution. Combining the infinite number (1/2) in pairs further gives the expression in the axiom. So
, or otherwise 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + ... = ∞.

However, it is also easy to show that the sum of the members of a series does not always give infinite results. For example, divide the interval between zero and one by the rational 1 / 2n series, that is, halve the intervals closer to zero, respectively. Obviously, the total length does not change if I divide the interval into several parts. It can be seen that the length of the obtained subintervals corresponds exactly to the rational division point of the end of the obtained subinterval closer to zero. That is, the length of the total interval is nothing but the sum of the lengths of the divided infinite number of intervals, which is the sum of the infinite number of members of the rational series except the first, zero (single-valued) term. So, soInfinite sums made up of members of series are simply called infinite series. If the sum of the row is finite, the row is called convergent, otherwise the row is divergent.

 The above operations, that is, the inclusion of an infinite number of members of a series (not just in the case of summation) in a mathematical operation, are called boundary formation, and the result is called a boundary. But the concept of limit training is used in mathematical analysis in other interpretations than just series. Above we have extended the boundary of the summation to infinity, but we can use other notations to extend finite arithmetic expressions to infinity in the same sense:It can be seen that we do not actually perform an infinite number of operations, because for us, this being impossible for finite beings, we infer the end result in detours, so in this case we have assigned an infinite algorithm, that is, a sequence, to divide the end result interval. These detours can be very diverse, they may require some intuition, we may not even find one, and then we will not be able to set a limit. Sometimes we don’t explicitly use the word thresholding while actually doing thresholding. In the examples above, for example, the sum of the members of the series is simply called a row, and the sum of the row is referred to as the result of the limit formation, while only three dots at the end of the sums indicate that we have to count an infinite number of members. If it doesn’t cause misunderstandings, we often omit summary boundaries, such as:

We must then see that if we want to know the members of a series in a set, we must form a union of the sets of members, and infinitely. So the set of the plurality generator series is:

In this we can express the last member of the infinite union with exactly the infinite sum in the last axiom, so the set undoubtedly contains the infinite, because we form the union according to exactly the same indexing and we form the last member:
∅ ∪ ∅⁺ ∪ … {1+1+1+...} = ∅ ∪ ∅⁺ ∪ … {∞} = {S}

This result has rather inconvenient consequences. An object that is not a finite natural number and is not subject to the arithmetic of natural numbers is included in the set, and even the application of elementary set operations to the set has become questionable. Only the operation of succession is valid for the infinitely large member, since according to the new axiom the successor of the infinite large member is also infinitely large. So we don’t have an infinite member either, but the number of infinitely large members is also infinite. Infinitely large members have neither a beginning nor a finishing element, no smallest or largest element, and no order can be defined between them. This represents another hitherto undiscussed value that is called innumerable infinites, because it is not possible to index infinitely large terms with finite indices. In connection with this, the relation of this new value to the former countable infinity arises as to whether it is greater than it. Since the plurality of an infinite set is defined as the plurality of sets that include sequences, the innumerable infinity used for the sets is considered to be a larger plurality than the countable infinity used for the plurality of series. This is because members with a finite index correspond to countable infinity, and members with a larger infinity index are not assigned a finite index, so they cannot be mapped to each other.

At least with a series of natural numbers. But the question arises as to what is the case with the set formed from the convergent series examined earlier. The members added to the queue are getting smaller and smaller, and it seems obvious that the members with infinitely high indexes appearing in the limit no longer add anything to the amount, i.e. they are the same. Thus, this means a single element in the set, the inclusion of a limit, which does not give a numerical difference from the countable infinite number of the series. Therefore, the countable infinite number of sets formed from convergent series is equal to the number of series. The different multiplicity of the index set (set formed from a series of natural numbers) and the set of the convergent series is also evident from the fact that it is not possible to create a one-to-one correspondence between infinitely large infinite index members and a single limit.

 Convergent series whose limit is zero are called zero series, and there can be an innumerable infinite number of them, because we cannot even formulate general enumeration principles for their enumeration. If we add any number to each member of such a series, the series will remain convergent and the limit of that series will be this added number.

Set of real numbers

Due to the introduction of the concept of infinite sets, the set operations defined for finite sets at the beginning of the article should be extended to infinite cases, which has no particular obstacle. However, it should not be forgotten that if we use all the elements of an infinite set in an operation (ΠΣ∪∩), it can only be done by boundary formation, either explicitly or implicitly. And with the exception of convergent series (or sets of them), this is an innumerable element. This property becomes especially important for sets containing a series of natural numbers (divergent).

For the concept of plurality, we have defined the set of plurality generators. This produced sets representing all finite manifold sets, to which we also assigned the notion of natural numbers. It is countably infinite from sets of finite numbers, and this is another notion of multiplicity, to which the innumerable infinity of sets containing divergent series has added. With that, we talked about every possible multiplicity.

About past incorrect statements.

You can perform operations with series or members of series, which can be divided into two main groups.

1. From a selected member of one or more series, a new series is formed by an operation. The result of the operations is thus another series, the members of which can be almost arbitrary mathematical objects (numbers, sets, series). Traditional mathematics uses this as the definition of a series, but in reality it is only a mapping between series that can obviously define specific series, but not affect the concept of a series, which is defined by the axioms of a series of natural numbers.

2. All members of one or more series form a finite number of numbers, sets, or sets of innumerable numbers by the limit of an operation.

Traditional mathematics is unable to separate the two cases, the formalism of set operations covers both cases, and many times even trained mathematicians are unaware that the candidate set operation defines only operations between members or implicitly interpreting a computing of limit. Many times they don’t even realize the problem of whether an infinite union or an infinite intersection includes computing of limit.

Power set concept: The set of all possible subsets of a set A is called a power set, denoted now: H (A). A power set can only be assigned to a set, not to a series.

The cardinality of the power set of a set n with finite n numbers is 2ⁿ, that is, each new element in the base set doubles the cardinality of the power set. The power set of a finite set is also finite.

But what about the innumerable infinite sets? On the one hand, the power set of such a set cannot be constructed because it cannot be counted either. If a set cannot be counted, then there is no function that can separate the set into its elements, and in this case not all possible subsets of its elements can be created. On the other hand, if, going beyond this unconstructiveness, and we assume that power sets of innumerable infinite sets exist (after all, imagination is limitless), they would likewise be cardinality innumerable infinity.

But what about the series? They can be assigned a power series in which the number of subsets representing the series members is doubled by the addition of each base series member, that is, it follows the logic of finite cases. That is, the cardinality of power series of series with countable infinite numbers is also countably infinite. As a result of the doubling, there is an obvious one-to-one correspondence between the series numbers of the local values ​​of the numbers written in the binary number system and the natural numbers, where each of the given place values ​​means the inclusion of the given number in the subset. Call this a place-value mapping function, noting that unless otherwise mentioned, these are place-values ​​of a number written in the binary number system.

But what about sets containing convergent series? For such sets, another element containing the limit must be added as the penultimate element (with an index of -1), and since this set can thus be treated as a series, its power series must be formed similarly to the series.

The most common objection is based precisely on the misunderstanding that many are not accustomed to, or do not even know, the distinction between concepts of the power set and the power series. The power set is assigned to a set, and the power series is assigned to a series. Only a series can be assigned to a series in one sense (bijective), so that each series member is assigned something else in a sense (bijective), such as the power set of the member. It is meaningless to interpret the concept of a power set in a series, because the series is different and the definition of the set is different, one-to-one correspondence between them cannot be interpreted.

The usual misinterpretation of the power set interpreted on series is the possible number of different series that can be formed from the series members. Their cardinality are indeed innumerable infinity, even just cardinality of real numbers, but this interpretation does not meet the definition of cardinality or power series. According to the definition of cardinality, if there exists a series that contains all members of the power series, then the power series can be counted. So the question is not how many series of sets can be defined using the members, but whether there is at least one series of sets that touches all subsets that can be made up of all series members. A power series is a single assignment on a given series. The concept of series made up of series members is a completely separate definition, which is completely confused with the concept of subsets made up of members of a series. In principle, subseries that can be formed from a series do not contain finite subsets either, since they do not form a series, the series always means an infinite term. The number of series is innumerable, the subsets are countable. Each of the innumerable series has power series, each of which is a countable series. Countless series cannot be defined by matching on a series, since the series has countable numbers to which only series with countable numbers can be associated. Only the computing of limit allows the derivation of a series of innumerable numbers.

Some people miss that, for example, the power sequence of natural numbers does not assign a finite sequence number to the sequence of even numbers by the said local-value mapping function. But this shortcoming has nothing to do with the notion of the power set. The series of even numbers has its own power series, and it is also a subseries of the power series of natural numbers. All possible groupings of finite members are fully counted by the locality-value matching function.

But what about Cantor's proof? Cantor misinterpreted a series of natural numbers as a set, thus implicitly (without Cantor's knowledge) generating an innumerable infinite cardinality set, and whose power set he tried to prove to be innumerable infinity cardinality. So it is not because of the proof that the power set became innumerable, but because the initial set was already such, and thus it would have been proved that the power sets of infinite (innumerable) sets are innumerable infinite . Cantor could not properly define the concept of the power set either, he could not distinguish the power series from the power set, just as he could not distinguish the series from the infinite set. But as I wrote in my Russel-Cantor analogy article, the proof indirectly contains a contradiction, a faulty logical scheme, which is accordingly successfully contradictory. If indirection dissolved, the statement takes the paradoxical form that a given set consists of elements that are not in it. And this contradiction has nothing to do with objects, sets, power sets, mappings that convey logic. An interesting moment of this proof, however, is that this logical contradiction can be resolved, and it just proves that since there are infinitely many finite cardinality, the set formed from the above S series of finite cardinality also contains infinite cardinality, so the set contains an element that does not match any element in the series by definition.

When does the previous theory make a mistake? Theories of cardinality can go in the trash. The infinity of infinite cardinality does not exist, there are only two kinds of infinity, the infinity of series or sets of convergent series, and the infinity of sets of divergent series. It makes further mistakes when someone juggles a ‘set’ of natural numbers like Cantor, referring to complementary sets with respect to the whole set because can there are unwanted infinitely large numbers in the whole set. Except in these cases, it is of no particular significance to treat the series as a set, although we will never see the numbers as they really are.

When the Russell paradox, and the existence of other logical paradoxes, came to light, many mathematicians thought that naive set theory was unsustainable, and immediately published a host of new axiomatic approaches, some of which were also rooted in mathematics. But there are two serious problems with these. This is one that they did not notice the logical error of treating the series as a set, so they themselves are at fault. On the other hand, they did not take into account the results of Gödel's theorems, that is, their previous expectation to rule out the existence of paradoxes and contradictory statements with no axioms and definitions was without any basis. Mathematics is a language, just like spoken languages, and there is not, it is not possible to create a meaningful language in which one cannot lie. Language is not a substitute for thinking, but a tools for the expression of thoughts.

Infinitely large natural numbers

How do we understand that, according to my previous articles, the set of finite natural numbers is an open set? Consider the 1 / n series. As the values ​​of n increase, they become closer and closer to zero, and the limit of the series is zero. If we consider the members of the series, or the non-zero finite natural numbers in the interpretation range of the function 1 / n, then zero is not included in the function values, they are taken from the open set (0, 1]. The whole set of natural numbers (except zero) is taken as the interpretation range, so the set of values ​​also takes the value zero, ie they come from the closed interval [0, 1], in addition, in the case of innumerable infinite numbers. the difference between the terms 0 <x <∞ and 0 <x, where in the second case x can be infinite (if we do not assume that x is a real number), that is, closed and open sets can be distinguished even at unlimited intervals.

What is the ratio of cardinality of finite and infinite large numbers? The shadow of the infinite ladder best illustrates this, which can also be understood as a one-dimensional projection of the Peano curve. The figure shows the mapping between the index series and the projection set and how this changes in the limit.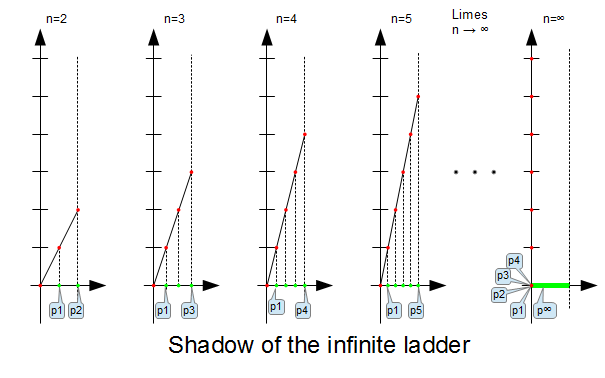

It is known that renowned irrational constants can only be defined as rational approximations, that is, with a quotients of two natural numbers. The more accurate the approximation, the larger these natural numbers. The irrational number sought is the limit of these series, so irrational numbers can be interpreted as quotients of two infinitely large integers. These, of course, are not clearly defined, as any fraction can be arbitrarily expanded.

With the previously mentioned local-value mapping function, we can map a clearly defined infinite number to the value set of virtually any integer series. Thus, even numbers, odd numbers, square numbers, and prime numbers also have a definite infinite number, each of which has finite place-valued digits. Thus, the local-value correspondence function can be extended, we can correspond the 2-ad notation of infinite numbers to subsets and series of integers.

Infinite numbers have been known in mathematics before, for more than a hundred years, as one form of p-adic numbers, and of which other forms are rational numbers. Of course, p-adic numbers only cover infinite numbers that can be written periodically according to some prime number-based number system p. This part of infinite numbers is thus countable cardinality, as opposed to non-periodic infinite numbers.

Substantial differences from previously prevalent theories

The usual definitions of numbers also include an additional axiom, according to which there is a set containing natural numbers (ZF, ZFC axiom systems, infinity axiom). Having said this as an axiom, the question has not arisen in many that this may be a logically lame axiom, since the axiom does not have to be proved, so everyone feels relieved to prove the consistency of the axiom system. As seen above, there can be many sets that contain finite natural numbers, but these sets also contain other types of objects, such as infinitely large numbers, or an open set whose complementary set is not empty. In fact, this axiom is thus completely superfluous, since the operation of succession alone can determine which sets can contain natural numbers, since a clearly defined series also clearly defines its limit (if it exists) and, on the other hand, suggests a misconception from natural numbers. Traditional mathematics is incapable of distinguishing between a series and the concept of a set containing a series, unnaturally and logically erroneously taking these two radically different (created in different ways) objects as identical, so it is unable to account for their differences.

Since the said axiom systems are the foundations of current mathematics, their inherent error extends or may extend to all current mathematical statements. Due to their axiom, the rules of mathematical proofs do not apply to it, as axioms do not have to be proved, so of course they cannot be refuted by regular mathematical proofs. Therefore, the detection of the error is also possible only through an alternative axiomatic structure, which is thus much more comprehensive than proving the error of a faulty theorem. Unfortunately, mathematicians today, detached from reality, interpret the concept of axioms as a completely independent statement, thus becoming unable to understand what the relationship is between mathematics and reality. Yet this has been known since Euclid. The axiom is a simple statement whose truth content is so obvious and self-evident that we have no need to prove its truth content, leaving no doubt as to their truth content. It is no coincidence that when, after more than one and a half thousand years, doubts arose as to one of the axioms of Euclid, its universal interpretation was also rejected. On the same basis, the axiom of infinity should not have been born either, since the definition of series is not the same as the definition of sets, and its axiomatic identification is not self-evident, or even, as can be read here, erroneous.

The standard definition of a series is also incorrect, according to which "a series is a function interpreted on a set of natural numbers". The logic is set on top of your head here. Instead of the axiomatic fixation of the principle of total induction in series, which is the basis of mathematical proofs, the series are built on a confusing set axiom, and thus induction.

Later, new axiom systems were born of natural numbers, but they did not overcome this problem either, in contrast, they raised the most basic foundations of mathematics to an academic level that practically pulls the ground out of mathematics. With this, mathematics became an abstract spiritualist meditation rather than a solid foundation of the sciences.

The usual definition of sets states the existence of power sets as an axiom. This is also a gross error, since it is a simple consequence of how to form subsets of the elements of a set using the defined set operations, and whether the set of all possible subsets can exist. Moreover, no one can construct a power set for a set with continuum cardinality, precisely because they are elements innumerable, so it is doubtful from the outset that such a power set can be considered existing or not, it can only be discussed as an assumption.

The so-called naive set theory is abundantly sufficient for an exact discussion of mathematics. Later, naive set theory was discarded with demands that could not be met later, and it even became certain that this demand could not be met. This was another reason for the introduction of new axiom systems, which again only complicated things that should be as simple as possible, as we have known since Euclid. The academic complexity of axioms is one of the root causes of errors in the most basic foundations of mathematics.

There is an area of ​​mathematics that discusses the cardinality of sets and rests on the faulty Cantorian theorem of the larger cardinality of the power set. This single theorem states that infinite numbers also form an infinite series, there is no other alternative possibility of obtaining certainty. These areas represent the blind track of mathematics due to the error of the basic theorem, unless there are structures to which these theories can be fitted, i.e. they can be placed on another foundation. It is fortunate that no major mathematical branch, no major theorem, is built on cardinality arithmetic. I think the reason for this is that the logic of mathematics also works subconsciously in the minds of mathematicians, and this affects our conscious thinking even if a faulty theorem credits us with the opposite. Or, more simply, false logic is unthinkable, untraceable.