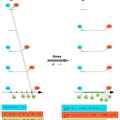
The Russell paradox:
Consider the set G which complete collection of all sets which not contains itself. Was this collection set G contains the itself? The question is undecidable. In fact, if not included, then this is a set that is not self-contained, so is the location of the G set. But if that's included, then G has no place in the G set.
Mathematical markup:
Let G = { g : g ∉ g }.
Then G ∈ G => G ∉ G, a contradiction.
Furthermore G ∉ G => G ∈ G, which is also a contradiction.
And since one of these two cases must be present, so the discrepancy can not be avoided, so the definition is incorrect, so there is no set which contain all sets which not contains itself.
The Cantor's theorem proof:
In Cantor's proof assumed the existence a function f(n) that is an assignment between an set A of elements and their subsets. This mapping is one-to-one function between set A and his power set H(A) on request by the definition of the same cardinality. Cantor's proof is included in a set X, which is the set of elements x ∈ A, which are not included in the corresponding f(x) subset. X = { x : x ∈ A x ∉ f (x) }. But if set X is an element of power set H(A), then must be exist an element x ∈ A such that f (x) = x, but this is contrary to the definition of the set X.
Analogy:
The set X corresponds to G set. Indeed any element n ∈ A corresponds a reference to subset N=f(n) by this one-to-one mapping. Therefore definition of set X corresponds definition of the sets that is not self-referenced inside set A. Thus, there is two difference in the analogy, which not affect the essence. First, in Cantor's proof limited to only set A. Second, words changed from “not self-referenced” to “not self-contained”. But the analogy is means that exist correspondence between the two examples, and therefore reference corresponds to contain. The logic of paradox is irrelevant. And of course, Cantor argues exactly the same as Russell, that is definitions of set of not self-contained sets leads to a contradiction. The analogy is immediately apparent if I'm writing self-contradictory definition of the set X of Cantor item:
X = { x : x ∈ A ˄ x ∉ X=f(x) }
This simplified (A and f(x) omitted):
X = { x : x ∉ X }
he contradiction is obvious: the X elements, which are not elements of X.
The replacement“not self-referenced” to “not self-contained” was already known . The Russel paradox can interpreted as library catalogs self-reference.
Contemporary conclusions:
Russell interpreters that the naive set theory contains a contradiction, therefore, to reject the use.
Cantor opinion that f(n) mapping does not exist, so the power set can not be same cardinality with base set.
In my conclusions:
Nothing wrong to naive set theory. The contradiction in the formulation of a paradox, and not in the set theory. If the condition of the containment is the not containment, it is a controversial requirement, and this is nothing to do with the argument or set theory just a false statement. In formal terms, G = {g: g ∉ G} expression is contradiction, and this fact leads to contradictions in the case paradoxes of Russell and Cantor's theorem. The contradiction in the Russell paradox appear only, if G = g. The contradiction eliminated, if prohibit this case, so G = { g : g ∉ g ˄ g ≠ G } is correct, and see clear the contradiction, if only see this case: g = { g : g ∉ g }.
The proof of Cantor's theorem claims with Russell paradox, but the paradox is not refers to any power set such detection of contradiction cannot be inferred to the existence of mapping related with power set. Only role of the function is to be using formulated Russell paradox problem. The mapping f(n) ensures of the elements usage as subsets. Therefore the Cantor's theorem is not proved.
The claim against the set theory as to can not be make the false statement is same, as it should not be lie in human language. Unrealistic single-valued logic. There is no place in mathematics.
Budapest, 12 april 2013 Takács Ferenc bp.