!!! In January 2025, I made significant discoveries and changes to my theory, so not all of the statements described here are true. I have only left my previous articles to illustrate the development of my thinking. !!!
Abstract: I show that the set of natural numbers, because incorrect definitions (axioms), it is not countable, so it is continuum cardinality, in contrast to previous assumptions, and intentions, that set of natural numbers it is countably infinite. The natural numbers used as set is not contain only countable non-negative finite integers, but also contain the class of uncountable infinite numbers. It follows that the countably infinite cardinality natural numbers can not form a mathematical set. I show also that the power set of natural numbers just are not a mathematical set, just as the natural numbers can not, but they are just infinite countable subsets such as natural numbers. Furthermore, I show the errors of proof of Cantor's theorem.
Keys: natural number, Peano's axiom, cardinality, power set, Cantor's theorem, refutation, disproof, dementi, rebuttal.
Introduction: The Giuseppe Peano's axioms published in 1889 is not yet call the natural numbers to set. In your axioms define natural numbers infinite followed each other and principle of mathematical induction, which allows proofs in number theory. Two years later the Georg Cantor's theorem published, and use the natural numbers as a set. No one is disturbed in the past 121 years that the set of natural numbers is treated as incorrect, but it can be a source of serious errors. This is best seen in Cantor's theorem, and its consequences are also incorrect. Meanwhile, is reformulated Peano's axioms, using the set theory, so now it is readable incorrectly in the books. Of course, the set theory is a great blessing for mathematics, because it gives easily use, and formalized tools. But hidden dangers in the use of sets, especially in case of infinite sets. In these traps, which have the greatest mathematicians were unable to avoid
Current status:
One of the current versions of the Peano's axioms in simple words:
(P1) zero is a natural number,
(P2) every natural number has a follower natural number (also known as successor),
(P3) zero is not the follower of any natural number,
(P4) if the followers two numbers are equal, then the numbers are equal,
(P5) if a set contains zero, and contain the followers of every element, then the set contain all natural numbers.
I note that the axioms freeing from the incorrect formalism become absolutely correct again, even if the fifth axiom is ambiguous.
Here are Cantor's proof, also in simple words:
We assume that the power set of natural numbers is countable, thus there exists a one-to-one correspondence f(n) to mapping the natural numbers, and this power set, therefore, all possible subsets of natural numbers to assign a number to mapping by the function f(n). Then we take the subset X, which is derived from n natural numbers, which does not contain the appropriatef(n) subset. So if, say, 5 is not element of the fifth subset, then 5 element of X subset.X is element of power set, therefore must be exist a x number such that f(x) = X, but there is no x such that f(x) = X, follows from definitions of X. The evident contradiction, which implies that the wrong with the starting assumption. Thus Cantor believes that, the power set is not countable. Cantor's theorem is formulated in general, the cardinality of a set less than the cardinality of his power set. The proof is similar, because countability not used in the proof. I will turn to the general case only in the last part tangentially, because I primarily the case of natural numbers I want to deal with.
The power set of natural numbers countable
For evidence of same cardinality is sufficient to show the existence of an one-to-one function between natural numbers and they power set. Here is a concrete function. Look at the binary representation of a given n natural numbers, and the associate to it n-th subset, H(n). Description of n the two digits are used, 0 and 1. The 1 digit on a place-value with given serial number is mapped to occurrence the natural number in given n-th subset. Here is few subsets with their serial numbers:
H(0) = H(000(2)) = {-,-,-} = {},
H(1) = H(001(2)) = {-,-,0} = {0},
H(2) = H(010(2)) = {-,1,-} = {1},
H(3) = H(011(2)) = {-,1,0} = {0,1},
H(4) = H(100(2)) = {2,-,-} = {2},
H(5) = H(101(2)) = {2,-,0} = {0,2},
H(6) = H(110(2)) = {2,1,-} = {1,2},
H(7) = H(111(2)) = {2,1,0} = {0,1,2},…,
H(15) = H(1111(2)) = {0,1,2,3},...,
H(31) = H(11111(2)) = {0,1,2,3,4}, ...
This mapping is also well-known earlier, and was so much one-to-one function that there is nothing to prove it. The place-values so countable as the natural numbers. In computing, this mapping just allows to the set operations implement as bitwise logical operations. You can disproof me if proof ones from the next three things. Show at least a subset which had no serial number, or show at least one serial number, which not belong to a subset, or show that this mapping no one-toone function.
Of course, the power set of natural numbers even so should not be used as a set as the natural numbers. As I show in the next section, this can be a source of serious errors. You can work with only finite numbers and finite size subset of finite numbers, and the statements of finite case extendible only by mathematical induction to all case of natural numbers. The mathematical induction is not a set operation.
This mapping usable for any other countable infinity object types, as rational numbers, etc., because these one-to-one mappable to natural numbers.
After this only it is not clear to me that light of this trivial could how to maintain a claim of Cantor's theorem so far. Cantor really proof that there can not exist the by him used function, but incorrect conclusion get he from this. But before turning to this, must be clear another question.
The set of finite natural numbers does not exist
In any finite subset of natural numbers there is always a largest component, and follower of the largest component is not component of the subset, and the it infinite next follower either not component of the subset too (Item 1). If the subset is anon-zero initial slice, that is, contained every natural number from one to the largest element, then largest component is equal with the number of elements, that is number of elements is element of subset (Item 2). When it declared that such a set exists with all natural numbers, in axiom P5, then we are forced to use the item 2. The number of natural numbers is infinite, so infinite is element is this set (Item 3). (deleted and inserted the following paragraph, nov, 2016)
The successor operation a natural number refers to another natural number, followed by another endless series of natural numbers. With this action either, but not allavailable numbers. Infinite natural number could not be obtained after any number of application this operation. However, the axiom(P5) raises the possibility that exist a set that contains all the natural numbers, but the successor operation can not be created it. I wonder how to create this set? Similar problems described us Zeno's paradox. To address this challenge limiting process serves for both Zeno paradox of both the set of all the natural numbers. When members of an infinite series each is required to perform an operation, we need the limit of sequence. N . However, the cluster thus produced contains not only the finite natural number, but also the infinite numbers, because the last element of the above operations is
So when someone refers to a set of natural numbers, that is refers to a set that contain every natural number, inevitably implies a reference to infinite numbers. Any subset of natural numbers can not contains all natural numbers, so no way to extend the subsets to all finite natural numbers by followers, or mathematical induction. There is no middle ground. If you are saying that infinite number can not the elements of this set, then this would also say that number of natural numbers is finite. Or if you are saying that not exist infinite natural numbers, then constitute the set should be completed on a finite before infinite, but it will only finite subset of natural numbers.
Of course we have to know from the infinite, a uncountably infinite cardinality set is. Any infinite number has uncountably infinite follower. So when we are performed operations with set of all natural numbers, then working with a set, which contain uncountable infinite numbers. Moreover, infinite numbers are an overwhelming majority because of the finite numbers will be negligible compared to the infinite.
This unfortunate circumstance is not bonded to the axioms, so axioms misunderstood, misleading, incomplete.
Prescribing the infinite numbers correspond to reciprocal of decimal representation of smaller than one positive real numbers, mirroring the decimal point. They have an infinite sequence of digits (three dots indicate) to the left of finite digits. Example the ...00 means those infinite numbers which divisible by hundred. Indeed any such fraction from (0,1) interval can be assigned to same series of digits in reverse order, as infinite integer. And because the infinite series properly represent the real numbers from (0,1) interval, so this reciprocal properly represent infinite positive integers, furthermore they cardinality same also, uncountably infinite.
So keep in mind that the much-talked-about set N continuum cardinality, and contain infinity numbers. Maybe write comfortable in a proof that n∈N, or n∉N, but this is misleading because ∞∈Ν, and therefore if n is infinite then formulas become mostly meaningless. Only the correct, if write that “n a natural number” or that “there is no natural number n”.
Unfortunate result that should re-forming the mathematical formalism. Introducing a relatively simple symbolic set I = N\{∞} and replacing N by I the most of earlier formulas are would logical correctness. Of course not really set I and there is a limited operations of set it performed.
Some remarks on the Cantor's theorem
Cantor's theorem is disproved that I showed a one-to-one mapping between natural numbers and they power set. So here I analyze only where Cantor was wrong. Using the mine H(n) mapping in the proof of Cantor verifiable that the set X contains all natural numbers, because serial number of subsets is always larger than the largest element in subsets. Thus, the set X equals the set of natural numbers, and assign to x number of the last, largest finite natural numbers would be if there were any. Instead x is infinite, and shows that Cantor calculate with infinite numbers. Before Cantor in the history of mathematics no one trying to handle the natural numbers as set with infinite numbers, and it is high time to realize that this is still not free to do so. The number theory problems may be prove only by induction and other methods on base of induction.*
Cantor's theorem is not limited to natural numbers, but it is considered apply to any sets, independently they cardinality. Indeed this item is considered evidence that cardinality not be exhausted cardinality of the natural numbers and real numbers but exist infinite series of infinite cardinality also. This is a mistake. The existence of a one-to-one mapping proof the equal cardinality of two set, but does not prove the non-existence of one-to one mapping the different cardinality. Just to say that non-exist one-to-one mapping at different cardinalty. The non-existence of a mapping possible other reasons. Especially when we are dealing with uncountable infinity set. However this is the case. As I show, in the countable infinity case exist one-to-one mapping. A set uncountable if non-exist one-to-one mapping between set and natural numbers. It is very likely that the same reason, there is non-exist mapping between the set and its power set (conjecture).
Illustrative example: Find a power set and a mapping on the real numbers. Interval [0,1] is sufficient to deal because an interval may mapping to the whole real line. Divide the interval equal parts n, where n is integer, and train the power set of n interval according the above H mapping.
Then the n subdivision assigned 2n index, and the same number not continuous interval. Try to train the limit properties of this subdivision as n approaches to infinity.
What then can we get results? The length of the intervals limit is zero and intervals really became a real number and they constantly cover the [0,1] interval. (We see similar coverage at Peano curve.) The H-mapping trends rather special. All finite natural numbers mapping to zero, to the interval left side. The other parts of interval mapped by infinite natural numbers. Indeed reciprocal of each finite number tends to zero, so they limit is zero. However, this mapping not one-to-one mapping yet, because all finite natural number mapped to only zero. The situation is even worse in evolution of power set because it not convergent. The power sets of different subdivisions independent of each other. So this example shows what difficulties, if referring to power set of an uncountable set, or try mapping that. Very likely that the insurmountable difficulties. Therefore, the use of the concept powerset is not justified at uncountable sets. Even more unjustified to assign function to this suspicious set. We found no solution, but the strength of our faith that there is no solution.
This example illustrates too that countable cardinality dwarfed to zero by comparison with uncountable cardinality. In contrast, for the larger cardinalities, there is no reality, no examples. This was only a mistaken hipothesys. There is no greater cardinality than cardinality of the real numbers.
This example illustrates too that the natural number declarig to set implies a limit training, because the infinite numbers do not get by induction. I should show this in another example.
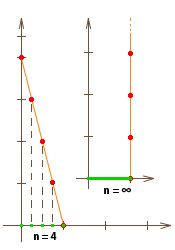
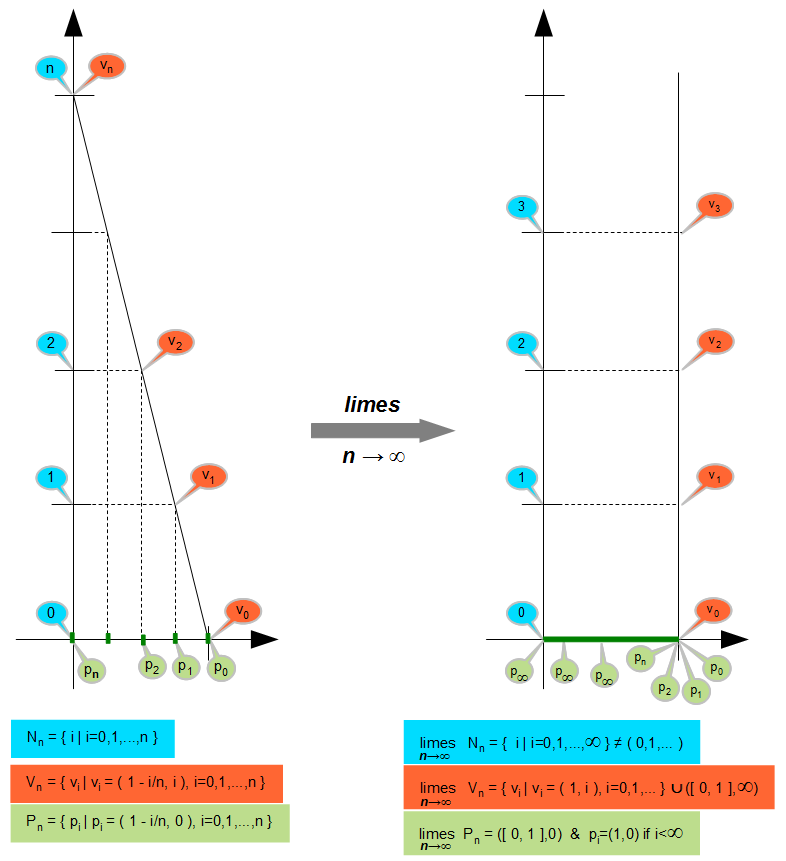
One more example: (The infinite ladder) Set up symbolic ladders (as well theoretical sections of their, so a series of point on straight sections) into point coordinates (1,0) so that relies to the y-axis. All ladders are always so long that reach the y-axis at positive integer values and the ladder rungs y coordinates are always integers. The ladders indexed according the y-intersection, so the n-th ladder is the set of point on line with y = n -nx equation between y-axis and x-axis in the integer y coordinate points. Examine the vertical projections the ladder rungs to x-axis. These points is (k/n, 0) coordinates at the n-th ladders, where (k = 0, ..., n). Let's examine what it will converge to series of ladders, the ladder rungs projection and y coordinates of a set of rungs, when we have infinite n. Increases n, the ladder is getting steeper and converges to the vertical so that the limit is a vertical point series above point (1,0). The the distance between projections of rungs 1/n that converges to zero, so the limit is zero, so that limit of projection of the ladder continuously covers the [0,1] real interval. The y coordinates of ladder rungs are starting-slice sets of natural numbers, and limit this includes all finite natural numbers. But not only them. It is any finite natural number k projection 1k/n converges to 1, when n trend from k to infinity, so that limit every rungs with finite index lay above the once (1,0) projection point. Consequently to the rest of [0,1] interval, which is [0,1) interval, falls only projection of the infinite integers indexed rungs. So this infinite natural numbers is necessary element of domain set. This example shows very clearly is that of an infinite series only will become to set by training limit operations, but during this the countably infinite series become continuum cardinality.
One more conclusion: Prompts the question of what is needed in the fifth axiom. Some sources suggest that the induction is intended to declare. If this were the case, it makes a very bad way. An axiom can only be good if it is self-evident and can be the basis of the elementary mathematics education. Very useful if we know which operations can be carried out on the finite set, but serious error when natural numbers are considered as set. This is not an elementary mathematics, not the level of axioms.
Budapest, 21 may 2012 Takács Ferenc bp.
* As I highlighted in detail in my later articles, Cantor's proof in every detail exactly equivalent with the Russell paradox, and the very reason we call this bucking to logical paradox because it is from logically contradictory assumption get a logically contradictory result. Indeed, Cantor trying create a set which may be contain only the components which may not be contain, so this a controversial condition. In this way easy to show that these sets do not exist, but this has nothing to do with to prove the theorem, and even set theory not. A simple logical error.